22. Optimalizace až na cost

Naučíme se optimalizovat funkce. Začneme od čisté implementace v Pythonu, zkusíme vyřešit problém v NumPy. Poté si ukážeme, jak postupně přejít k jazykům nižší úrovně, jako je Fortran nebo C, a také si představíme balík Numba.

from IPython.display import Image

import matplotlib.pyplot as plt
import numpy as np

22.1. Základní koncepce optimalizace

Už víme, že Python je jazyk, ve kterém jde velice efektivně programovat. A díky balíkům, jako jsou NumPy, SciPy nebo SymPy jde velice rychle řešit různé vědecké úlohy. Je pochopitelné, že s takovouto mírou abstrakce může být výsledný program pomalejší, než kdyby byl dobře napsán v nějakém kompilovaném jazyce typu C/C++ nebo Fortran. Musíme si ovšem uvědomit, že efektivita programu se měří v celkovém čase stráveném na vývoji a běhu programu (pro daný soubor úloh). Schématicky můžeme znázornit závislost rychlosti běhu programu v závislosti na délce vývoje asi takto:

Image(filename='optimizing-what.png')

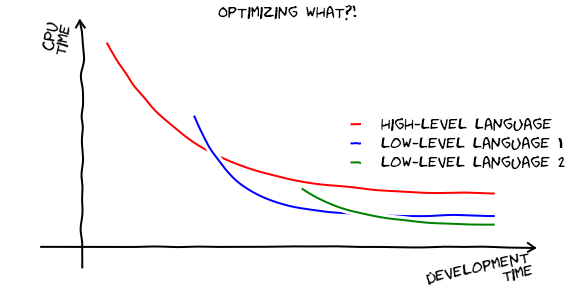
Všimněte si například, že typicky existuje nějaký offset ve vývojovém čase, tj. trvá nám déle v nízkoúrovňovém jazyce, než vůbec dostaneme první výsledek. Potřeba optimalizace tedy silně závisí na objemu výpočtů, které budeme s daným programem řešit.

Toto ovšem neznamená, že pokud je objem velký, máme hned začít programovat v C nebo Fortranu. Za chvíli si ukážeme, jak optimalizaci řešit chytřeji a postupně. Empirické pravidlo říká, že 90 % výpočetního času zabere 10 % zdrojového kódu. Jedná se o konkrétní příklad obecného Paretova 80 / 20 principu. Je tedy vhodné nejprve těchto 10 % najít a poté je teprve začít optimalizovat. Python nám k tomuto účelu poskytuje velice mocné nástroje.

22.2. Profilování

Profilování je nástroj, který nám umožní najít kritická místa v našem programu, oněch 10 %, které stojí za to optimalizovat. Zkusme si to ukázat na jednoduchém příkladu.

def heavy_calc(X):
    Y = X.copy()
    for i in range(10):
        Y = Y**i
    return Y

def heavy_loop(inputs):
    res = []
    for X in inputs:
        res.append(heavy_calc(X))
    return res

def code_setup():
    from numpy.random import rand
    N = 20
    M = 1000
    print("Will generate {} random arrays".format(N))
    inputs = [rand(M, M) for n in range(N)]
    print("Will calculate now")
    result = heavy_loop(inputs)
    print("Finished calculation")

Python obsahuje dva základní mofuly pro profilování - profile a cProfile, z nichž ten druhý je rychlejší. Pomocí funkce run pustíme výpočet pod dohledem cProfile, výsledky uložíme do souboru.

import cProfile
cProfile.run('code_setup()', 'pstats')

Will generate 20 random arrays
Will calculate now
Finished calculation

Dále budeme potřebovat modul pstats, který nám umožní s výsledky pracovat. Použije k tomu třídu Stats.

from pstats import Stats
p = Stats('pstats')

print_stats nám zobrazí prvních n záznamů.

p.print_stats(10)

Sun Jan 19 13:23:06 2025    pstats

         3892 function calls (3755 primitive calls) in 0.537 seconds

   Random listing order was used
   List reduced from 378 to 10 due to restriction <10>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
       13    0.000    0.000    0.000    0.000 /Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/_distutils_hack/__init__.py:101(find_spec)
       25    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/enum.py:1551(__or__)
       17    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/enum.py:1562(__and__)
        3    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/threading.py:1155(_wait_for_tstate_lock)
      126    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/enum.py:1544(_get_value)
        4    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/json/encoder.py:183(encode)
        2    0.000    0.000    0.000    0.000 /Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/_distutils_hack/__init__.py:108(<lambda>)
        1    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/re/__init__.py:226(compile)
       58    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/enum.py:726(__call__)
        1    0.000    0.000    0.000    0.000 /Users/kuba/.local/share/uv/python/cpython-3.12.5-macos-aarch64-none/lib/python3.12/functools.py:35(update_wrapper)

<pstats.Stats at 0x1061c1100>

Ty jsou ovšem nesetříděné. Následující výstup už je užitečnější, záznamy jsou totiž setříděné podle celkového času stráveného v dané funkci. Navíc strip_dirs odstraní adresáře ze jmen funkcí.

p.strip_dirs().sort_stats('cumulative').print_stats(10)

Sun Jan 19 13:23:06 2025    pstats

         3892 function calls (3755 primitive calls) in 0.537 seconds

   Ordered by: cumulative time
   List reduced from 378 to 10 due to restriction <10>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        8    0.079    0.010    0.762    0.095 base_events.py:1909(_run_once)
      4/1    0.000    0.000    0.530    0.530 {built-in method builtins.exec}
       20    0.416    0.021    0.431    0.022 2469674079.py:1(heavy_calc)
        1    0.000    0.000    0.320    0.320 2469674079.py:13(code_setup)
        1    0.000    0.000    0.320    0.320 2469674079.py:7(heavy_loop)
       20    0.015    0.001    0.015    0.001 {method 'copy' of 'numpy.ndarray' objects}
     13/1    0.000    0.000    0.014    0.014 <frozen importlib._bootstrap>:1349(_find_and_load)
     13/1    0.000    0.000    0.014    0.014 <frozen importlib._bootstrap>:1304(_find_and_load_unlocked)
     12/1    0.000    0.000    0.014    0.014 <frozen importlib._bootstrap>:911(_load_unlocked)
      3/1    0.000    0.000    0.014    0.014 <frozen importlib._bootstrap_external>:989(exec_module)

<pstats.Stats at 0x1061c1100>

Takto vypadá výstup setříděný pomocí nekumulovaného času.

p.sort_stats('time').print_stats(10)

Sun Jan 19 13:23:06 2025    pstats

         3892 function calls (3755 primitive calls) in 0.537 seconds

   Ordered by: internal time
   List reduced from 378 to 10 due to restriction <10>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
       20    0.416    0.021    0.431    0.022 2469674079.py:1(heavy_calc)
        8    0.079    0.010    0.762    0.095 base_events.py:1909(_run_once)
       20    0.015    0.001    0.015    0.001 {method 'copy' of 'numpy.ndarray' objects}
      7/0    0.011    0.002    0.000          {method 'control' of 'select.kqueue' objects}
        9    0.007    0.001    0.007    0.001 {built-in method _imp.create_dynamic}
      9/6    0.002    0.000    0.006    0.001 {built-in method _imp.exec_dynamic}
     35/2    0.001    0.000    0.012    0.006 <frozen importlib._bootstrap>:480(_call_with_frames_removed)
      9/8    0.001    0.000    0.002    0.000 events.py:86(_run)
       36    0.001    0.000    0.001    0.000 {built-in method posix.stat}
       24    0.000    0.000    0.000    0.000 socket.py:626(send)

<pstats.Stats at 0x1061c1100>

Jupyter nám může usnadnit práci pomocí %prun a %%prun. Např.

%prun -s cumulative -l 10 code_setup()

Will generate 20 random arrays
Will calculate now
Finished calculation
 

         2184 function calls (2126 primitive calls) in 0.755 seconds

   Ordered by: cumulative time
   List reduced from 219 to 10 due to restriction <10>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.000    0.000    0.589    0.589 {built-in method builtins.exec}
        1    0.016    0.016    0.589    0.589 <string>:1(<module>)
       20    0.507    0.025    0.520    0.026 2469674079.py:1(heavy_calc)
    14/13    0.009    0.001    0.375    0.029 base_events.py:1909(_run_once)
        1    0.000    0.000    0.363    0.363 2469674079.py:13(code_setup)
        1    0.000    0.000    0.363    0.363 2469674079.py:7(heavy_loop)
       20    0.016    0.001    0.016    0.001 {method 'copy' of 'numpy.ndarray' objects}
    15/13    0.000    0.000    0.003    0.000 {method 'run' of '_contextvars.Context' objects}
        7    0.000    0.000    0.002    0.000 zmqstream.py:583(_handle_events)
        5    0.000    0.000    0.002    0.000 asyncio.py:200(_handle_events)

Z obou výstupů celkem jasně vydíme, že naprostou většinu času trávíme ve funkci heavy_calc. Pokud se tedy chceme pustit do optimalizace, musíme se zaměřit právě na tuto část našeho programu.

Výsledky můžete navíc spojit s nástroji pro vizualizaci, např.SnakeViz nebo vprof, popř. pokročilý editor jako PyCharm.

22.3. Vzorová úloha - vzdálenost množiny bodů ve vícerozměrném prostoru

(Tento příklad byl převzat z http://jakevdp.github.io/blog/2013/06/15/numba-vs-cython-take-2.)

Zadání je jednoduché: pro M bodů v N rozměrném prostoru spočítejte vzájemnou vzdálenost \(d\), která je pro dva body \(x,y\) definovaná jako \(\sqrt {\sum_{i=1}^N {{{\left( {{x_i} - {y_i}} \right)}^2}} } \). Výslekem je tedy (symetrická) matice \(M\times M\).

# toto nechť jsou naše vstupní data
M = 1000
N = 3
X = np.random.random((M, N))

Implementace v čistém Pythonu

Nemůžeme asi očekávat, že toto bude nejrychlejší a nejsnadnější verze našeho programu. Přesto stojí za to ji vyzkoušet, navíc ji budeme ještě potřebovat.

def pairwise_python(X):
    M = X.shape[0]
    N = X.shape[1]
    D = np.empty((M, M), dtype=float)
    for i in range(M):
        for j in range(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = np.sqrt(d)
    return D

Tahle funkce nám bude pomáhat ukládat výsledné časy z %timeit.

Do pairwise_times si uložíme výsledné časy.

pairwise_times = {}

timings = %timeit -o pairwise_python(X)
pairwise_times['plain_python'] = timings

1.13 s ± 68.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

To samé pomocí NumPy

V případě NumPy můžeme v tomto případě využít broadcasting. Celá funkce tak zabere jeden rádek.

def pairwise_numpy(X):
    return np.sqrt(((X[:, np.newaxis, :] - X) ** 2).sum(-1))

Zkusíme, jestli výsledky jsou stejné pomocí assert a numpy.allclose.

assert np.allclose(pairwise_numpy(X), pairwise_python(X), rtol=1e-10, atol=1e-15)

Výsledky jsou stejné až na velmi malé rozdíly - to je nebezpečí numerických výpočtů s konečnou přesností.

timings = %timeit -o pairwise_numpy(X)
pairwise_times['numpy'] = timings

18.3 ms ± 221 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Vidíme, že jsme zkrátili běh programu více než 100-krát. To není špatné, navíc je implementace daleko jednodušší.

Přichází Cython

Cython je nástroj, který z Python programu, obohaceného o nějaké Cython direktivy, vytvoří program v C (případně C++), který je možné zkompilovat a okamžitě použít jako modul v Pythonu. Typickým příkladem Cython direktiv jsou statické typy. Cython samozřejmě umožňuje používat funkce z binárních knihoven s C rozhraním.

Zkusíme optimalizovat naší funkci pairwise_python.

• Cython zdroják má koncovku .pyx (za začátku byl Pyrex).

• Cython dokáže přeložit jakýkoli Python. Výsledkem je ale minimální (nebo spíš žádná) optimalizace.

• cimport je analogie import, pracuje ale s Cython definicemi funkcí (.pxd soubory).

• Cython dodává numpy.pyx, obsahující dodatečné informace pro kompilace NumPy modulů. Proto voláme cimport numpy.

• Podobně libc je speciální modul Cythonu.

• Funkce se deklarují (moho deklarovat) se statickými typy vstupních parametrů. My použijeme np.ndarray[np.float64_t, ndim=2].

• Proměnné se deklarují pomocí cdef.

# Odkomentujte pro instalaci Cythonu
# !pip install cython

%%file cyfuncs.pyx

language_level = "3str"

import numpy as np
# numpy pro Cython
cimport numpy as np
from libc.math cimport sqrt

# tohle je čistý Python
def pairwise0(X):
    M = X.shape[0]
    N = X.shape[1]
    D = np.empty((M, M), dtype=float)
    for i in range(M):
        for j in range(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = np.sqrt(d)
    return D

# tady už začínáme optimalizovat, změny ale nejsou drastické
def pairwise1(np.ndarray[np.float64_t, ndim=2] X):
    cdef int M = X.shape[0]
    cdef int N = X.shape[1]
    cdef double tmp, d
    cdef np.ndarray D = np.empty((M, M), dtype=np.float64)
    for i in range(M):
        for j in range(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = sqrt(d)
    return D

Overwriting cyfuncs.pyx

%%file setup.py

from distutils.core import setup
from Cython.Build import cythonize
import numpy

setup(
  name='cyfuncs',
  include_dirs=[numpy.get_include()],
  ext_modules=cythonize("cyfuncs.pyx"),
)

Overwriting setup.py

!python setup.py build_ext --inplace

Compiling cyfuncs.pyx because it changed.
[1/1] Cythonizing cyfuncs.pyx
/Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/Cython/Compiler/Main.py:381: FutureWarning: Cython directive 'language_level' not set, using '3str' for now (Py3). This has changed from earlier releases! File: /Users/kuba/workspace/fjfi/python-fjfi/numerical_python_course/lecture_notes.cz/cyfuncs.pyx
  tree = Parsing.p_module(s, pxd, full_module_name)
In file included from cyfuncs.c:1240:
In file included from /Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/numpy/_core/include/numpy/arrayobject.h:5:
In file included from /Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/numpy/_core/include/numpy/ndarrayobject.h:12:
In file included from /Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/numpy/_core/include/numpy/ndarraytypes.h:1909:
/Users/kuba/workspace/fjfi/python-fjfi/.venv/lib/python3.12/site-packages/numpy/_core/include/numpy/npy_1_7_deprecated_api.h:17:2: warning: "Using deprecated NumPy API, disable it with "          "#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION" [-W#warnings]
   17 | #warning "Using deprecated NumPy API, disable it with " \
      |  ^
cyfuncs.c:8531:26: warning: code will never be executed [-Wunreachable-code]
 8531 |                 module = PyImport_ImportModuleLevelObject(
      |                          ^~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2 warnings generated.
ld: warning: search path 'Modules/_hacl' not found
ld: warning: search path '/install/lib' not found

Jak jsme již říkali, Cython vytvoří C zdroják, který se pak kompiluje pomocí běžného překladače (např. gcc). Pojďme se na tento soubor podívat.

from IPython.display import FileLink
FileLink('cyfuncs.c')

cyfuncs.c

Ten soubor je dlouhý … Obsahuje spoustu Python “balastu”, na kterém vidíme, jak je vlastně samotný CPython naprogramován. Naštěstí tento soubor obsahuje i komentáře, které říkají, které řádce daný blok odpovídá. Např.

 /* "cyfuncs.pyx":16
  *                 tmp = X[i, k] - X[j, k]
  *                 d += tmp * tmp
  *             D[i, j] = np.sqrt(d)             # <<<<<<<<<<<<<<
  *     return D
  * 
  */

import cyfuncs

print("cyfuncs obsahuje: " + ", ".join((d for d in dir(cyfuncs) if not d.startswith("_"))))

cyfuncs obsahuje: language_level, np, pairwise0, pairwise1

Podívejme se, jestli dostávám stále stejné výsledky.

assert np.allclose(pairwise_numpy(X), cyfuncs.pairwise1(X), rtol=1e-10, atol=1e-15)

No a jak jsme na tom s časem?

timings = %timeit -o cyfuncs.pairwise0(X)
pairwise_times['cython0'] = timings

1.13 s ± 41.7 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

timings = %timeit -o cyfuncs.pairwise1(X)
pairwise_times['cython1'] = timings

79.6 ms ± 3.5 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

IPython %%cython magic

IPython, tak jako v mnoha jiných případech, nám práci s Cythonem usnadňuje pomocí triku %%cython. Zkusíme ho použít. Zároveň zkusíme ještě více náš kód optimalizovat, zatím je totiž pomalejší než numpy.

%load_ext Cython

%%cython -a

import numpy as np
cimport numpy as np
cimport cython
from libc.math cimport sqrt

@cython.boundscheck(False)
@cython.wraparound(False)
def pairwise_cython(double[:, ::1] X):
    cdef int M = X.shape[0]
    cdef int N = X.shape[1]
    cdef double tmp, d
    cdef double[:, ::1] D = np.empty((M, M), dtype=np.float64)
    for i in range(M):
        for j in range(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = sqrt(d)
    return np.asarray(D)

Generated by Cython 3.0.11

Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.

 01: 

+02: import numpy as np

  __pyx_t_7 = __Pyx_ImportDottedModule(__pyx_n_s_numpy, NULL); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_7);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_np, __pyx_t_7) < 0) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_7); __pyx_t_7 = 0;
/* … */
  __pyx_t_7 = __Pyx_PyDict_NewPresized(0); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_7);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_test, __pyx_t_7) < 0) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_7); __pyx_t_7 = 0;

 03: cimport numpy as np

 04: cimport cython

 05: from libc.math cimport sqrt

 06: 

+07: @cython.boundscheck(False)

/* Python wrapper */
static PyObject *__pyx_pw_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_1pairwise_cython(PyObject *__pyx_self, 
#if CYTHON_METH_FASTCALL
PyObject *const *__pyx_args, Py_ssize_t __pyx_nargs, PyObject *__pyx_kwds
#else
PyObject *__pyx_args, PyObject *__pyx_kwds
#endif
); /*proto*/
static PyMethodDef __pyx_mdef_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_1pairwise_cython = {"pairwise_cython", (PyCFunction)(void*)(__Pyx_PyCFunction_FastCallWithKeywords)__pyx_pw_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_1pairwise_cython, __Pyx_METH_FASTCALL|METH_KEYWORDS, 0};
static PyObject *__pyx_pw_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_1pairwise_cython(PyObject *__pyx_self, 
#if CYTHON_METH_FASTCALL
PyObject *const *__pyx_args, Py_ssize_t __pyx_nargs, PyObject *__pyx_kwds
#else
PyObject *__pyx_args, PyObject *__pyx_kwds
#endif
) {
  __Pyx_memviewslice __pyx_v_X = { 0, 0, { 0 }, { 0 }, { 0 } };
  #if !CYTHON_METH_FASTCALL
  CYTHON_UNUSED Py_ssize_t __pyx_nargs;
  #endif
  CYTHON_UNUSED PyObject *const *__pyx_kwvalues;
  PyObject *__pyx_r = 0;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("pairwise_cython (wrapper)", 0);
  #if !CYTHON_METH_FASTCALL
  #if CYTHON_ASSUME_SAFE_MACROS
  __pyx_nargs = PyTuple_GET_SIZE(__pyx_args);
  #else
  __pyx_nargs = PyTuple_Size(__pyx_args); if (unlikely(__pyx_nargs < 0)) return NULL;
  #endif
  #endif
  __pyx_kwvalues = __Pyx_KwValues_FASTCALL(__pyx_args, __pyx_nargs);
  {
    PyObject **__pyx_pyargnames[] = {&__pyx_n_s_X,0};
  PyObject* values[1] = {0};
    if (__pyx_kwds) {
      Py_ssize_t kw_args;
      switch (__pyx_nargs) {
        case  1: values[0] = __Pyx_Arg_FASTCALL(__pyx_args, 0);
        CYTHON_FALLTHROUGH;
        case  0: break;
        default: goto __pyx_L5_argtuple_error;
      }
      kw_args = __Pyx_NumKwargs_FASTCALL(__pyx_kwds);
      switch (__pyx_nargs) {
        case  0:
        if (likely((values[0] = __Pyx_GetKwValue_FASTCALL(__pyx_kwds, __pyx_kwvalues, __pyx_n_s_X)) != 0)) {
          (void)__Pyx_Arg_NewRef_FASTCALL(values[0]);
          kw_args--;
        }
        else if (unlikely(PyErr_Occurred())) __PYX_ERR(0, 7, __pyx_L3_error)
        else goto __pyx_L5_argtuple_error;
      }
      if (unlikely(kw_args > 0)) {
        const Py_ssize_t kwd_pos_args = __pyx_nargs;
        if (unlikely(__Pyx_ParseOptionalKeywords(__pyx_kwds, __pyx_kwvalues, __pyx_pyargnames, 0, values + 0, kwd_pos_args, "pairwise_cython") < 0)) __PYX_ERR(0, 7, __pyx_L3_error)
      }
    } else if (unlikely(__pyx_nargs != 1)) {
      goto __pyx_L5_argtuple_error;
    } else {
      values[0] = __Pyx_Arg_FASTCALL(__pyx_args, 0);
    }
    __pyx_v_X = __Pyx_PyObject_to_MemoryviewSlice_d_dc_double(values[0], PyBUF_WRITABLE); if (unlikely(!__pyx_v_X.memview)) __PYX_ERR(0, 9, __pyx_L3_error)
  }
  goto __pyx_L6_skip;
  __pyx_L5_argtuple_error:;
  __Pyx_RaiseArgtupleInvalid("pairwise_cython", 1, 1, 1, __pyx_nargs); __PYX_ERR(0, 7, __pyx_L3_error)
  __pyx_L6_skip:;
  goto __pyx_L4_argument_unpacking_done;
  __pyx_L3_error:;
  {
    Py_ssize_t __pyx_temp;
    for (__pyx_temp=0; __pyx_temp < (Py_ssize_t)(sizeof(values)/sizeof(values[0])); ++__pyx_temp) {
      __Pyx_Arg_XDECREF_FASTCALL(values[__pyx_temp]);
    }
  }
  __PYX_XCLEAR_MEMVIEW(&__pyx_v_X, 1);
  __Pyx_AddTraceback("_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51.pairwise_cython", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __Pyx_RefNannyFinishContext();
  return NULL;
  __pyx_L4_argument_unpacking_done:;
  __pyx_r = __pyx_pf_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_pairwise_cython(__pyx_self, __pyx_v_X);
  int __pyx_lineno = 0;
  const char *__pyx_filename = NULL;
  int __pyx_clineno = 0;

  /* function exit code */
  __PYX_XCLEAR_MEMVIEW(&__pyx_v_X, 1);
  {
    Py_ssize_t __pyx_temp;
    for (__pyx_temp=0; __pyx_temp < (Py_ssize_t)(sizeof(values)/sizeof(values[0])); ++__pyx_temp) {
      __Pyx_Arg_XDECREF_FASTCALL(values[__pyx_temp]);
    }
  }
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}

static PyObject *__pyx_pf_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_pairwise_cython(CYTHON_UNUSED PyObject *__pyx_self, __Pyx_memviewslice __pyx_v_X) {
  int __pyx_v_M;
  int __pyx_v_N;
  double __pyx_v_tmp;
  double __pyx_v_d;
  __Pyx_memviewslice __pyx_v_D = { 0, 0, { 0 }, { 0 }, { 0 } };
  int __pyx_v_i;
  int __pyx_v_j;
  int __pyx_v_k;
  PyObject *__pyx_r = NULL;
/* … */
  /* function exit code */
  __pyx_L1_error:;
  __Pyx_XDECREF(__pyx_t_1);
  __Pyx_XDECREF(__pyx_t_2);
  __Pyx_XDECREF(__pyx_t_3);
  __Pyx_XDECREF(__pyx_t_4);
  __Pyx_XDECREF(__pyx_t_5);
  __PYX_XCLEAR_MEMVIEW(&__pyx_t_6, 1);
  __Pyx_AddTraceback("_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51.pairwise_cython", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __pyx_r = NULL;
  __pyx_L0:;
  __PYX_XCLEAR_MEMVIEW(&__pyx_v_D, 1);
  __Pyx_XGIVEREF(__pyx_r);
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}
/* … */
  __pyx_tuple__22 = PyTuple_Pack(9, __pyx_n_s_X, __pyx_n_s_M, __pyx_n_s_N, __pyx_n_s_tmp, __pyx_n_s_d, __pyx_n_s_D, __pyx_n_s_i, __pyx_n_s_j, __pyx_n_s_k); if (unlikely(!__pyx_tuple__22)) __PYX_ERR(0, 7, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_tuple__22);
  __Pyx_GIVEREF(__pyx_tuple__22);
/* … */
  __pyx_t_7 = __Pyx_CyFunction_New(&__pyx_mdef_54_cython_magic_72b25b6e366aa2ac2fa9f6e8b1834b878e03df51_1pairwise_cython, 0, __pyx_n_s_pairwise_cython, NULL, __pyx_n_s_cython_magic_72b25b6e366aa2ac2f, __pyx_d, ((PyObject *)__pyx_codeobj__23)); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 7, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_7);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_pairwise_cython, __pyx_t_7) < 0) __PYX_ERR(0, 7, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_7); __pyx_t_7 = 0;

 08: @cython.wraparound(False)

 09: def pairwise_cython(double[:, ::1] X):

+10:     cdef int M = X.shape[0]

  __pyx_v_M = (__pyx_v_X.shape[0]);

+11:     cdef int N = X.shape[1]

  __pyx_v_N = (__pyx_v_X.shape[1]);

 12:     cdef double tmp, d

+13:     cdef double[:, ::1] D = np.empty((M, M), dtype=np.float64)

  __Pyx_GetModuleGlobalName(__pyx_t_1, __pyx_n_s_np); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  __pyx_t_2 = __Pyx_PyObject_GetAttrStr(__pyx_t_1, __pyx_n_s_empty); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_2);
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
  __pyx_t_1 = __Pyx_PyInt_From_int(__pyx_v_M); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  __pyx_t_3 = __Pyx_PyInt_From_int(__pyx_v_M); if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_3);
  __pyx_t_4 = PyTuple_New(2); if (unlikely(!__pyx_t_4)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_4);
  __Pyx_GIVEREF(__pyx_t_1);
  if (__Pyx_PyTuple_SET_ITEM(__pyx_t_4, 0, __pyx_t_1)) __PYX_ERR(0, 13, __pyx_L1_error);
  __Pyx_GIVEREF(__pyx_t_3);
  if (__Pyx_PyTuple_SET_ITEM(__pyx_t_4, 1, __pyx_t_3)) __PYX_ERR(0, 13, __pyx_L1_error);
  __pyx_t_1 = 0;
  __pyx_t_3 = 0;
  __pyx_t_3 = PyTuple_New(1); if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_3);
  __Pyx_GIVEREF(__pyx_t_4);
  if (__Pyx_PyTuple_SET_ITEM(__pyx_t_3, 0, __pyx_t_4)) __PYX_ERR(0, 13, __pyx_L1_error);
  __pyx_t_4 = 0;
  __pyx_t_4 = __Pyx_PyDict_NewPresized(1); if (unlikely(!__pyx_t_4)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_4);
  __Pyx_GetModuleGlobalName(__pyx_t_1, __pyx_n_s_np); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  __pyx_t_5 = __Pyx_PyObject_GetAttrStr(__pyx_t_1, __pyx_n_s_float64); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_5);
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
  if (PyDict_SetItem(__pyx_t_4, __pyx_n_s_dtype, __pyx_t_5) < 0) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_5); __pyx_t_5 = 0;
  __pyx_t_5 = __Pyx_PyObject_Call(__pyx_t_2, __pyx_t_3, __pyx_t_4); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_5);
  __Pyx_DECREF(__pyx_t_2); __pyx_t_2 = 0;
  __Pyx_DECREF(__pyx_t_3); __pyx_t_3 = 0;
  __Pyx_DECREF(__pyx_t_4); __pyx_t_4 = 0;
  __pyx_t_6 = __Pyx_PyObject_to_MemoryviewSlice_d_dc_double(__pyx_t_5, PyBUF_WRITABLE); if (unlikely(!__pyx_t_6.memview)) __PYX_ERR(0, 13, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_5); __pyx_t_5 = 0;
  __pyx_v_D = __pyx_t_6;
  __pyx_t_6.memview = NULL;
  __pyx_t_6.data = NULL;

+14:     for i in range(M):

  __pyx_t_7 = __pyx_v_M;
  __pyx_t_8 = __pyx_t_7;
  for (__pyx_t_9 = 0; __pyx_t_9 < __pyx_t_8; __pyx_t_9+=1) {
    __pyx_v_i = __pyx_t_9;

+15:         for j in range(M):

    __pyx_t_10 = __pyx_v_M;
    __pyx_t_11 = __pyx_t_10;
    for (__pyx_t_12 = 0; __pyx_t_12 < __pyx_t_11; __pyx_t_12+=1) {
      __pyx_v_j = __pyx_t_12;

+16:             d = 0.0

      __pyx_v_d = 0.0;

+17:             for k in range(N):

      __pyx_t_13 = __pyx_v_N;
      __pyx_t_14 = __pyx_t_13;
      for (__pyx_t_15 = 0; __pyx_t_15 < __pyx_t_14; __pyx_t_15+=1) {
        __pyx_v_k = __pyx_t_15;

+18:                 tmp = X[i, k] - X[j, k]

        __pyx_t_16 = __pyx_v_i;
        __pyx_t_17 = __pyx_v_k;
        __pyx_t_18 = __pyx_v_j;
        __pyx_t_19 = __pyx_v_k;
        __pyx_v_tmp = ((*((double *) ( /* dim=1 */ ((char *) (((double *) ( /* dim=0 */ (__pyx_v_X.data + __pyx_t_16 * __pyx_v_X.strides[0]) )) + __pyx_t_17)) ))) - (*((double *) ( /* dim=1 */ ((char *) (((double *) ( /* dim=0 */ (__pyx_v_X.data + __pyx_t_18 * __pyx_v_X.strides[0]) )) + __pyx_t_19)) ))));

+19:                 d += tmp * tmp

        __pyx_v_d = (__pyx_v_d + (__pyx_v_tmp * __pyx_v_tmp));
      }

+20:             D[i, j] = sqrt(d)

      __pyx_t_19 = __pyx_v_i;
      __pyx_t_18 = __pyx_v_j;
      *((double *) ( /* dim=1 */ ((char *) (((double *) ( /* dim=0 */ (__pyx_v_D.data + __pyx_t_19 * __pyx_v_D.strides[0]) )) + __pyx_t_18)) )) = sqrt(__pyx_v_d);
    }
  }

+21:     return np.asarray(D)

  __Pyx_XDECREF(__pyx_r);
  __Pyx_GetModuleGlobalName(__pyx_t_4, __pyx_n_s_np); if (unlikely(!__pyx_t_4)) __PYX_ERR(0, 21, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_4);
  __pyx_t_3 = __Pyx_PyObject_GetAttrStr(__pyx_t_4, __pyx_n_s_asarray); if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 21, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_3);
  __Pyx_DECREF(__pyx_t_4); __pyx_t_4 = 0;
  __pyx_t_4 = __pyx_memoryview_fromslice(__pyx_v_D, 2, (PyObject *(*)(char *)) __pyx_memview_get_double, (int (*)(char *, PyObject *)) __pyx_memview_set_double, 0);; if (unlikely(!__pyx_t_4)) __PYX_ERR(0, 21, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_4);
  __pyx_t_2 = NULL;
  __pyx_t_20 = 0;
  #if CYTHON_UNPACK_METHODS
  if (unlikely(PyMethod_Check(__pyx_t_3))) {
    __pyx_t_2 = PyMethod_GET_SELF(__pyx_t_3);
    if (likely(__pyx_t_2)) {
      PyObject* function = PyMethod_GET_FUNCTION(__pyx_t_3);
      __Pyx_INCREF(__pyx_t_2);
      __Pyx_INCREF(function);
      __Pyx_DECREF_SET(__pyx_t_3, function);
      __pyx_t_20 = 1;
    }
  }
  #endif
  {
    PyObject *__pyx_callargs[2] = {__pyx_t_2, __pyx_t_4};
    __pyx_t_5 = __Pyx_PyObject_FastCall(__pyx_t_3, __pyx_callargs+1-__pyx_t_20, 1+__pyx_t_20);
    __Pyx_XDECREF(__pyx_t_2); __pyx_t_2 = 0;
    __Pyx_DECREF(__pyx_t_4); __pyx_t_4 = 0;
    if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 21, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_5);
    __Pyx_DECREF(__pyx_t_3); __pyx_t_3 = 0;
  }
  __pyx_r = __pyx_t_5;
  __pyx_t_5 = 0;
  goto __pyx_L0;

assert np.allclose(pairwise_numpy(X), pairwise_cython(X), rtol=1e-10, atol=1e-15)

timings = %timeit -o pairwise_cython(X)
pairwise_times['cython2'] = timings

1.98 ms ± 40.3 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Tohle je už konečně výrazné zrychlení oproti NumPy.

Cython toho nabízí mnoho

Podívejte se na http://docs.cython.org co všechno Cython nabízí – není toho málo, např.

• použití C++

• šablony (templates)

• OpenMP (k tomu se možná ještě dostaneme)

• vytváření C-API

• třídy (cdef classes)

Z Fortranu (nebo C) do Pythonu pomocí F2PY

F2PY je nástroj, který byl v podstatě vytvořen pro NumPy a SciPy, protože, jak dobře víme, tyto moduly volají externí knihovny napsané ve Fortrane nebo C. Dokumentaci (trochu zastaralou) najdeme zde. Bylo tedy velice výhodné vytvořit nástroj, který toto usnadní. A tak se zrodilo F2PY. Ve zkratce, F2PY umožňuje velice jednoduše z Fortran nebo C funkcí vytvořit Python modul. Využívá navíc vlastností NumPy pro předávání vícerozměnrých polí.

Poďme chvilku programovat ve Fortranu :)

%%file pairwise_fort.f90

subroutine pairwise_fort(X, D, m, n)
    integer :: n,m
    double precision, intent(in) :: X(m, n)
    double precision, intent(out) :: D(m, m)
    integer :: i, j, k
    double precision :: r

    do j = 1,m
        do i = 1,m
            r = 0
            do k = 1,n
                r = r + (X(i,k) - X(j,k)) * (X(i,k) - X(j,k))
            end do
            D(i,j) = sqrt(r)
        end do
    end do
end subroutine pairwise_fort

Overwriting pairwise_fort.f90

Z čeho f2py bere informace o vytvoření modulu?

1. Pole (double precision) převádí na numpy array.

2. intent(in) = vstupní argument.

3. intent(out) = výstupní argument.

4. f2py schová explicitně zadané rozměry polí (m, n).

Pokud bychom programovali v C, je potřeba dodat f2py nějaké informace navíc, neboť např. intent v C neexistuje.

Tento soubor přeložíme pomocí f2py:

!f2py -c pairwise_fort.f90 -m pairwise_fort

Cannot use distutils backend with Python>=3.12, using meson backend instead.
Using meson backend
Will pass --lower to f2py
See https://numpy.org/doc/stable/f2py/buildtools/meson.html
Reading fortran codes...
	Reading file 'pairwise_fort.f90' (format:free)
Post-processing...
	Block: pairwise_fort
			Block: pairwise_fort
Applying post-processing hooks...
  character_backward_compatibility_hook
Post-processing (stage 2)...
Building modules...
    Building module "pairwise_fort"...
    Generating possibly empty wrappers"
    Maybe empty "pairwise_fort-f2pywrappers.f"
        Constructing wrapper function "pairwise_fort"...
          d = pairwise_fort(x,[m,n])
    Wrote C/API module "pairwise_fort" to file "./pairwise_fortmodule.c"
The Meson build system
Version: 1.6.1
Source dir: /private/var/folders/dm/gbbql3p121z0tr22r2z98vy00000gn/T/tmp5ugidbi4
Build dir: /private/var/folders/dm/gbbql3p121z0tr22r2z98vy00000gn/T/tmp5ugidbi4/bbdir
Build type: native build
Project name: pairwise_fort
Project version: 0.1
Fortran compiler for the host machine: gfortran (gcc 14.2.0 "GNU Fortran (Homebrew GCC 14.2.0_1) 14.2.0")
Fortran linker for the host machine: gfortran ld64 1115.7.3
C compiler for the host machine: cc (clang 16.0.0 "Apple clang version 16.0.0 (clang-1600.0.26.6)")
C linker for the host machine: cc ld64 1115.7.3
Host machine cpu family: aarch64
Host machine cpu: aarch64
Program /Users/kuba/workspace/fjfi/python-fjfi/.venv/bin/python3 found: YES (/Users/kuba/workspace/fjfi/python-fjfi/.venv/bin/python3)
Found pkg-config: YES (/opt/homebrew/bin/pkg-config) 2.3.0
Run-time dependency python found: YES 3.12
Library quadmath found: YES
Build targets in project: 1

Found ninja-1.11.1.git.kitware.jobserver-1 at /Users/kuba/workspace/fjfi/python-fjfi/.venv/bin/ninja
INFO: autodetecting backend as ninja
INFO: calculating backend command to run: /Users/kuba/workspace/fjfi/python-fjfi/.venv/bin/ninja -C /private/var/folders/dm/gbbql3p121z0tr22r2z98vy00000gn/T/tmp5ugidbi4/bbdir
ninja: Entering directory `/private/var/folders/dm/gbbql3p121z0tr22r2z98vy00000gn/T/tmp5ugidbi4/bbdir'
[3/6] Compiling Fortran object pairwis...in.so.p/pairwise_fort-f2pywrappers.f.o
f951: Warning: Nonexistent include directory '/install/include/python3.12' [-Wmissing-include-dirs]
[4/6] Compiling Fortran object pairwis...on-312-darwin.so.p/pairwise_fort.f90.o
f951: Warning: Nonexistent include directory '/install/include/python3.12' [-Wmissing-include-dirs]
[6/6] Linking target pairwise_fort.cpython-312-darwin.sorc_fortranobject.c.o

-m pairwise_fort je požadované jméno modulu. Můžeme ho rovnou importovat, resp. jeho stejnojmennou funkci.

from pairwise_fort import pairwise_fort
print(pairwise_fort.__doc__)

d = pairwise_fort(x,[m,n])

Wrapper for ``pairwise_fort``.

Parameters
----------
x : input rank-2 array('d') with bounds (m,n)

Other Parameters
----------------
m : input int, optional
    Default: shape(x, 0)
n : input int, optional
    Default: shape(x, 1)

Returns
-------
d : rank-2 array('d') with bounds (m,m)

Fortran a C používají jiné uspořádání paměti pro ukládání vícerozměrných polí. Fortran je “column-major” zatímco C je “row-major”. NumPy dokáže pracovat s obojím a pro uživatele je to obvykle jedno. Pokud ovšem chceme předat vícerozměrné pole do Fortran funkce, je lepší mít prvky uložené v paměti jako to dělá Fortran. V takovém případě totiž f2py předá pouze referenci (ukazatel) na dané místo v paměti. V opačném případě f2py nejprve pole musí transponovat, tj. vytvořit kopii s jiným uspořádáním, což může být samozřejmě náročné na pamět a procesor.

Vytvoříme si proměnnou XF, která má Fortran uspořádání, pomocí numpy.asfortranarray (prozaický název :)

XF = np.asfortranarray(X)

Vyzkoušíme, jestli stále dostáváme stejné výsledky.

assert np.allclose(pairwise_numpy(X), pairwise_fort(X), rtol=1e-10, atol=1e-15)

No a konečně se můžeme podívat, jak je to s rychlostí …

timings = %timeit -o pairwise_fort(X)
pairwise_times['fortran'] = timings

2.43 ms ± 251 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

22.4. Představuje se numba

Numba kompiluje Python kód pomocí LLVM. Podporujme just-in-time kompilaci pomocí dekorátoru jit (http://numba.pydata.org/numba-doc/latest/user/jit.html).

@numba.jit(
    signature=None, 
    nopython=False, 
    nogil=False, 
    cache=False, 
    forceobj=False, 
    parallel=False, 
    error_model='python', 
    fastmath=False, locals={}
)

# Odkomentujte pro instalaci balíku Numba
# !pip install numba

import numba

pairwise_numba = numba.jit(pairwise_python)

Tradiční kontrola. Po prvním spuštění navíc Numba funkci poprvé zkompiluje.

assert np.allclose(pairwise_numpy(X), pairwise_numba(X), rtol=1e-10, atol=1e-15)

Jaký čas od takto “jednoduché” optimalizace můžeme očekávat?

timings = %timeit -o pairwise_numba(X)
pairwise_times['numba'] = timings

2.48 ms ± 65 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Vidíme, že zrychlení je výborné - jsme na úrovni zatím nejlepšího výsledku! A navíc že jsme toho dosáhli jediným řádkem (kromě importů).

Ještě můžeme zkusit výledek vylepšit pomocí paralelizace, nopython a / nebo fastmath režimu. Pro nopython musíme vytvořit výsledný numpy objekt vně kompilované funkce. Paralelizace docílíme pomocí parallel=True a numba.prange. Všimněte si použití @jit jako dekorátoru.

@numba.jit(nopython=True, parallel=True, fastmath=True)
def _pairwise_nopython(X: np.ndarray, D: np.ndarray) -> np.ndarray:
    M = X.shape[0]
    N = X.shape[1]
    for i in numba.prange(M):
        for j in numba.prange(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = np.sqrt(d)
    return D


def pairwise_numba_fast_parallel(X: np.ndarray) -> np.ndarray:
    D = np.empty((X.shape[0], X.shape[0]), dtype = float)
    _pairwise_nopython(X, D)
    return D

assert np.allclose(pairwise_numpy(X), pairwise_numba_fast_parallel(X), rtol=1e-10, atol=1e-15)

timings = %timeit -o pairwise_numba_fast_parallel(X)
pairwise_times['numba_fast_parallel'] = timings

711 μs ± 33.1 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

22.5. Pojdme počítat na GPU i CPU: JAX

JAX: High-Performance Array Computing poskytuje plnou paletu nastrojů pro výpočty jak na CPU, tak na GPU.

Mezi jeho hlavní výhody patří:

• NumPy-like API - JAX podporuje většinu NumPy operací.

• JIT kompilace - JAX umožňuje, podobně jako numba, kompilaci funkcí pomocí jax.jit.

• Běží všude - stejný kód může běžet na CPU, GPU i TPU.

• Automatická diferenciace - JAX umožňuje výpočet gradientů a Hessiánů.

# Odkomentujte pro instalaci balíku JAX
# !pip install jax[cpu] jaxlib

JAX NumPy API je téměř identické s NumPy API. Jediný rozdíl je, že JAX funkce vrací vlastní datovy typ, které reprezentují pole na určitém zařízení (CPU, GPU, TPU).). Je proto vyhodné importovat JAX jako import jax.numpy as jnp společně s NumPy jako import numpy as np.

import jax.numpy as jnp
import jax

V případě, že bychom měli dostupné GPU (AMD/NVIDIA), vyděli bychom jej v nasledujícím seznamu.

jax.devices()

[CpuDevice(id=0)]

Pro zpřístupnění vypočtů na GPU stačí nahradit np za jnp a JAX se postará o zbytek.

def pairwise_jax(X):
    return jnp.sqrt(jnp.power(X[:, jnp.newaxis, :] - X, 2).sum(-1))
    #return jnp.sqrt((jnp.power(X[:, jnp.newaxis, :] - X, 2)).sum(-1))

assert np.allclose(pairwise_numpy(X), pairwise_jax(X), rtol=1e-10, atol=1e-15)

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[50], line 1
----> 1 assert np.allclose(pairwise_numpy(X), pairwise_jax(X), rtol=1e-10, atol=1e-15)

AssertionError: 

Ouha, co je špatně? Jelikož GPU pracuje s nižší přesností, JAX pracuje v zakladním režimu float32 namísto float64.

pairwise_jax(X).dtype

dtype('float32')

Pro vypočty s 64-bitovou přesností je potřeba povolit jax_enable_x64.

from jax import config
config.update("jax_enable_x64", True)

pairwise_jax(X).dtype

dtype('float64')

assert np.allclose(pairwise_numpy(X), pairwise_jax(X), rtol=1e-10, atol=1e-15)

Proj JIT kompilaci stačí přidat dekorátor jax.jit.

Nicméně pozor:

• První volání funkce s JIT kompilací může byt pomalejší, než když bychom funkci volali bez kompilace.

• JIT vyžaduje znát typy a tvar (shape) vstupních parametrů v době kompilace.

@jax.jit
def pairwise_jax_jit(X):
    res = (jnp.sqrt((jnp.power(X[:, jnp.newaxis, :] - X, 2)))).sum(-1)
    return res

X_jnp = np.asarray(X, dtype=jnp.float64)

timings = %timeit -o pairwise_jax(X_jnp)
pairwise_times['jax'] = timings

10.7 ms ± 17 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

timings = %timeit -o pairwise_jax_jit(X_jnp)
pairwise_times['jax_jit'] = timings

663 μs ± 9.51 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

22.6. Srovnání výsledků

Výsledky můžeme porovnat pomocí grafu.

pairwise_times

{'plain_python': <TimeitResult : 1.13 s ± 68.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)>,
 'numpy': <TimeitResult : 18.3 ms ± 221 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)>,
 'cython0': <TimeitResult : 1.13 s ± 41.7 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)>,
 'cython1': <TimeitResult : 79.6 ms ± 3.5 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)>,
 'cython2': <TimeitResult : 1.98 ms ± 40.3 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)>,
 'fortran': <TimeitResult : 2.43 ms ± 251 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)>,
 'numba': <TimeitResult : 2.48 ms ± 65 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)>,
 'numba_fast_parallel': <TimeitResult : 711 μs ± 33.1 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)>,
 'jax': <TimeitResult : 10.7 ms ± 17 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)>,
 'jax_jit': <TimeitResult : 663 μs ± 9.51 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)>}

fig, ax = plt.subplots()
values = np.array([t.average for t in pairwise_times.values()])
x = range(len(pairwise_times))
ax.bar(x, values)
ax.set_xticks(x)
ax.set_xticklabels(tuple(pairwise_times.keys()), rotation='vertical')
ax.set_ylabel('time [ms]')
ax.set_yscale('log')

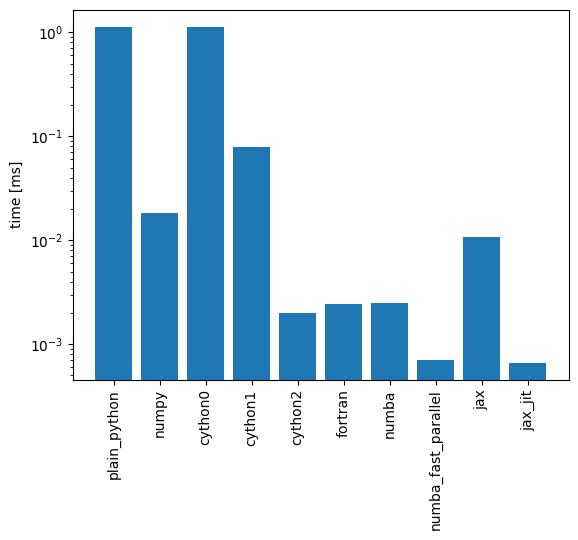
### Důkladnější srovnaní:
pairwise_functions = {
    'plain_python': pairwise_python,
    'numpy': pairwise_numpy,
    'cython0': cyfuncs.pairwise0,
    'cython1': cyfuncs.pairwise1,
    'cython2': pairwise_cython,
    'fortran': pairwise_fort,
    'numba': pairwise_numba,
    'numba_fast_parallel': pairwise_numba_fast_parallel,
    'jax': pairwise_jax,
    'jax_jit': pairwise_jax_jit
}

Ms = np.logspace(1, 3.5, 6).astype(int)
N = 3

paiwise_times_all = {}
for name, func in pairwise_functions.items():
    print(name)
    timings = []
    for M in Ms:
        X = np.random.random((M, N))
        print(M)
        # t = %timeit -o func(X)
        if "jax" in name:
            X_jnp = np.asarray(X, dtype=jnp.float64)
            # Přeskočíme první měření, protože probíha kompilace
            func(X_jnp)
            t = %timeit -o -r 2 func(X_jnp)
        else:
            t = %timeit -o -r 2 func(X)

        timings.append(t.average)

    paiwise_times_all[name] = timings

plain_python
10
111 μs ± 544 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
31
1.1 ms ± 45.6 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
100
11.4 ms ± 415 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
316
109 ms ± 658 μs per loop (mean ± std. dev. of 2 runs, 10 loops each)
1000
1.1 s ± 4.75 ms per loop (mean ± std. dev. of 2 runs, 1 loop each)
3162
11.2 s ± 51.6 ms per loop (mean ± std. dev. of 2 runs, 1 loop each)
numpy
10
3.96 μs ± 0.608 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
31
19 μs ± 527 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
100
208 μs ± 10.8 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
316
1.85 ms ± 1.49 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
1000
20.5 ms ± 382 μs per loop (mean ± std. dev. of 2 runs, 10 loops each)
3162
199 ms ± 3.42 ms per loop (mean ± std. dev. of 2 runs, 1 loop each)
cython0
10
106 μs ± 828 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
31
1.01 ms ± 13 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
100
10.3 ms ± 5.73 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
316
104 ms ± 71.3 μs per loop (mean ± std. dev. of 2 runs, 10 loops each)
1000
1.05 s ± 6.76 ms per loop (mean ± std. dev. of 2 runs, 1 loop each)
3162
10.6 s ± 110 ms per loop (mean ± std. dev. of 2 runs, 1 loop each)
cython1
10
6.62 μs ± 4.32 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
31
60.4 μs ± 9.07 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
100
623 μs ± 1.36 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
316
6.65 ms ± 48.7 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
1000
81.7 ms ± 2.61 ms per loop (mean ± std. dev. of 2 runs, 10 loops each)
3162
787 ms ± 20.3 ms per loop (mean ± std. dev. of 2 runs, 1 loop each)
cython2
10
982 ns ± 4.6 ns per loop (mean ± std. dev. of 2 runs, 1,000,000 loops each)
31
2.56 μs ± 1.39 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
100
17.1 μs ± 1.1 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
316
160 μs ± 93.1 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
1000
1.95 ms ± 1.53 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
3162
20.3 ms ± 193 μs per loop (mean ± std. dev. of 2 runs, 10 loops each)
fortran
10
501 ns ± 0.712 ns per loop (mean ± std. dev. of 2 runs, 1,000,000 loops each)
31
2.29 μs ± 2.48 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
100
20.4 μs ± 48.4 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
316
201 μs ± 680 ns per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
1000
2.32 ms ± 25.3 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
3162
22.8 ms ± 251 μs per loop (mean ± std. dev. of 2 runs, 10 loops each)
numba
10
604 ns ± 1.75 ns per loop (mean ± std. dev. of 2 runs, 1,000,000 loops each)
31
2.37 μs ± 3.2 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
100
20 μs ± 125 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
316
192 μs ± 1.5 μs per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
1000
2.39 ms ± 34.1 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
3162
24 ms ± 27.8 μs per loop (mean ± std. dev. of 2 runs, 10 loops each)
numba_fast_parallel
10
95.4 μs ± 126 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
31
96 μs ± 293 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
100
99.9 μs ± 19.5 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
316
140 μs ± 5.56 μs per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
1000
655 μs ± 762 ns per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
3162
5.7 ms ± 6.79 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
jax
10
43.3 μs ± 4.18 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
31
73.4 μs ± 1.52 μs per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
100
161 μs ± 557 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
316
1.41 ms ± 2.31 μs per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
1000
10.6 ms ± 1.3 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)
3162
128 ms ± 2.93 ms per loop (mean ± std. dev. of 2 runs, 10 loops each)
jax_jit
10
6.17 μs ± 12.4 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
31
17.4 μs ± 7.84 ns per loop (mean ± std. dev. of 2 runs, 100,000 loops each)
100
20.7 μs ± 19.4 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
316
99.5 μs ± 206 ns per loop (mean ± std. dev. of 2 runs, 10,000 loops each)
1000
649 μs ± 82.6 ns per loop (mean ± std. dev. of 2 runs, 1,000 loops each)
3162
6.1 ms ± 11.6 μs per loop (mean ± std. dev. of 2 runs, 100 loops each)

fig, ax = plt.subplots()

for name, times in paiwise_times_all.items():
    ax.plot(Ms, times, label=name)
    ax.set_xscale('log')
    ax.set_yscale('log')

ax.set_xlabel('M')
ax.set_ylabel('time [s]')

ax.legend()

<matplotlib.legend.Legend at 0x12cf32300>

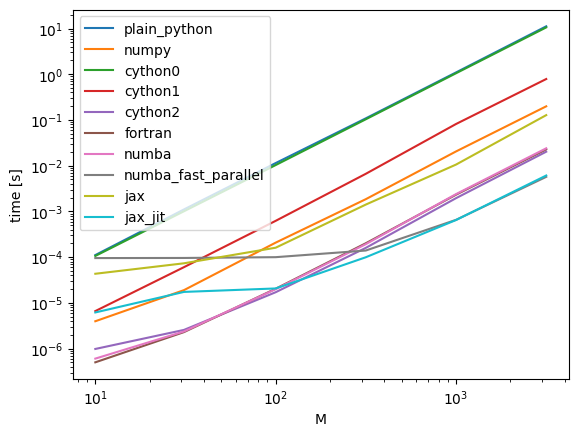
22.7. Další možnosti

• Vestavěný modul ctypes dovoluje volat funkce z externích dynamických knihoven. Pro použití s NumPy viz Cookbook.

• Alternativou k ctypes je cffi.

• CuPy využívá GPU.

• numexpr dokáže kompilovat Numpy výrazy.

• Theano se zaměřuje na strojové učení, také optimalizuje vektorové (maticové) operace, dovoluje je spouštět na CPU.

• Nuitka kompiluje Python, ale na rozdíl od Numba nespecializuje funkce na základě typů.

• SWIG jde použít pro propojení s mnoha jazyky.’

Cvičení

Obdobný postup aplikujte na výpočet kumulativního součtu, který je definovaný jako

\(\displaystyle S_j = \sum\limits_{i = 1}^j x_i \)

Výsledky a časování porovnejte s numpy.cumsum.

Nápověda: Ve vaší funkci vytvořte nejprve výsledné numpy pole pomocí numpy.empty_like.