21. Vědecká knihovna SciPy#
SciPy je základní referenční knihovnou, obsahující nástroje pro vědecké výpočty. Najdeme v ní např. speciální funkce, interpolace, Fourierovu transformaci, numerické integrátory a mnohé další. Naším cílem bude ukázat některé z funkcí SciPy.
Tento notebook byl z (velké) části převzat a přeložen z J.R. Johansson: Lectures on scientific computing with Python - díky.
21.1. Přehled SciPy#
SciPy staví na NumPy a poskytuje mnoho funkcí “vyšší úrovně” pro vědecké výpočty. Ve SciPy je asi dvacet modulů, každý z těchto modulů obsahuje mnoho funkcí a/nebo tříd pro danou oblast.
from IPython.display import IFrame
IFrame('http://docs.scipy.org/doc/scipy/reference/index.html', 900, 450)
21.2. Import SciPy#
# toto je typický import scipy
import scipy as sp
# a potřebujeme i numpy a matplotlib
import numpy as np
import matplotlib.pyplot as plt
21.3. Něco na zahřátí – speciální funkce#
Speciální funkce jsou často řešením vědeckých úloh. Jejich implementace je v mnoha případech poměrně náročná. Proto existují knihovny jako je scipy.special: http://docs.scipy.org/doc/scipy/reference/special.html#module-scipy.special.
Podíváme se např. na Besselovy funkce.
import scipy.special
Jednoduché vyčíslení funkcí s daným vstupem.
n = 0 # order
x = 0.0
# Bessel function of first kind
print("J_%d(%f) = %f" % (n, x, sp.special.jn(n, x)))
x = 1.0
# Bessel function of second kind
print("Y_%d(%f) = %f" % (n, x, sp.special.yn(n, x)))
J_0(0.000000) = 1.000000
Y_0(1.000000) = 0.088257
Funkce jsou samozřejmě vektorové, pomocí matplotlib si jednoduše nakreslíme graf.
x = np.linspace(0, 10, 100)
fig, ax = plt.subplots(1, 2, figsize=(16,4))
for i, (func, label) in enumerate(zip((sp.special.jn, sp.special.yn), (r"$J_%d(x)$", r"$Y_%d(x)$"))):
for n in range(4):
ax[i].plot(x, func(n, x), label=label % n)
ax[i].legend(loc="best")
ax[i].set_xlabel("x")
ax[i].set_ylim(-1, 1)
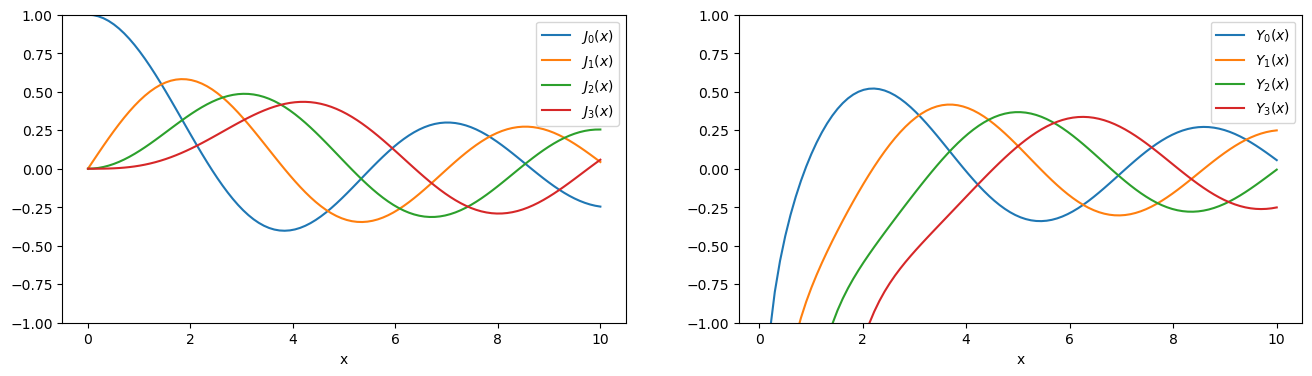
Zkusíme najít kořeny Besselových funkcí
n = 0 # order
m = 4 # number of roots to compute
sol = sp.special.jn_zeros(n, m)
print('Found roots:', sol)
# zkouška
print('This should be (almost) zero:', sp.special.jn(n, sol))
# využijeme allclose
print('Check using np.allclose:', np.allclose(sp.special.jn(n, sol), 0))
Found roots: [ 2.40482556 5.52007811 8.65372791 11.79153444]
This should be (almost) zero: [ 0.00000000e+00 -1.41172448e-17 1.04035365e-16 -1.77008254e-16]
Check using np.allclose: True
21.4. Numerická integrace#
Vyčíslení určitého integrálu#
Numerical evaluation of a function of the type Často potřebujeme numericky vyčíslit určitý integrál, tj.
\(\displaystyle \int_a^b f(x) {\rm d}x\)
Numerické integraci se často říká kvadratura, anglicky quadrature. Podle toho se jmenují o funkce v modulu scipy.integrate, např. quad, dblquad, tplquad nebo obecné nquad.
import scipy.integrate
Zkusíme spočítat jednodychý integrál:
\(\displaystyle \int_0^1 x {\rm d}x\)
val, abserr = sp.integrate.quad(lambda x: x, 0, 1)
print("výsledek = {:g} ± {:.2g}".format(val, abserr))
výsledek = 0.5 ± 5.6e-15
Můžeme dokonce pracovat s nekonečnými mezemi.
val, abserr = sp.integrate.quad(lambda x: np.exp(-x ** 2), -np.inf, np.inf)
print("výsledek = {:g} ± {:.2g}".format(val, abserr))
print("rozdíl od přesné hodnoty (√π) = {:g}".format(val - np.sqrt(np.pi)))
výsledek = 1.77245 ± 1.4e-08
rozdíl od přesné hodnoty (√π) = 0
Vícerozměrná integrace funguje podobně. Rozdíl je ovšem v tom, že vnitřní meze jsou obecně funkce vnějších proměnných. Tady k tomu využijeme anonymní (lambda) funkce.
def integrand(x, y):
return np.exp(-x**2 - y**2)
x_lower = 0
x_upper = 10
y_lower = 0
y_upper = 10
val, abserr = sp.integrate.dblquad(integrand, x_lower, x_upper, lambda x : y_lower, lambda x: y_upper)
print(val, abserr)
0.7853981633974476 1.3753098510206357e-08
# spočítáme obsah kruhu s daným poloměrem
r = 1 / np.sqrt(np.pi)
def integrand(x, y):
return 1
def y_upper(x):
return np.sqrt(r**2 - x**2)
def y_lower(x):
return -np.sqrt(r**2 - x**2)
val, abserr = sp.integrate.dblquad(integrand, -r, r, y_lower, y_upper)
print("výsledek = {:g} ± {:.2g}".format(val, abserr))
assert np.allclose(val, np.pi * r**2)
výsledek = 1 ± 6.4e-10
Obyčejné diferenciální rovnice (ODR)#
scipy.integrate (ano, řešení ODR je v tomto modulu, protože řešením ODR je určitý integrál) obsahuje odeint, které je jednodušší, a objektové rozhraní ode, které umožňuje větší kontrolu.
My teď použijeme odeint pro řešení rovnic dvojitého kyvadla.
ODR (nebo jejich soustava) je často zadaná jako
\(y' = f(y, t)\)
s počátečními podmínkami
\(y(t=0) = y_0\)
odeint pak lze použít jednoduše:
y_t = odeint(f, y_0, t)
kde t je předem zadané pole, ve kterých požadujeme řešení.
Příklad 1: jednoduché kyvadlo#
Rovnice jednoduchého gravitačního kyvadla (pro malou amplitudu) je
\(\displaystyle {\ddot \theta} + \frac{g}{L}\theta = 0\)
Řešení je jednoduché:
\(\displaystyle {\theta} = \theta_0 \cos\left( \sqrt{\frac{g}{L}} t \right) \)
Zkusme si tuto rovnici vyřešit numericky. Jelikož potřebujeme rovnice prvního řádu, definujeme vektor \(x = \left(\theta , \dot\theta \right)\), takže
\(\displaystyle {\dot x_1} = x_2\)
\(\displaystyle {\dot x_2} = - \frac{g}{L}\theta \)
import scipy.constants
L = 0.5
m = 0.1
def dx_pendulum(x, t):
"""
The right-hand side of the pendulum ODE
"""
theta, dtheta = x[0], x[1]
d_theta_dt = dtheta
d_dtheta_dt = - sp.constants.g / L * theta
return d_theta_dt, d_dtheta_dt
# počáteční stav
x0 = [np.pi / 8, 0]
# časy pro řešení
t = np.linspace(0, 10, 250)
# a konečně řešení
x = sp.integrate.odeint(dx_pendulum, x0, t)
# analytické řešení
x_anal = x0[0] * np.cos(np.sqrt(sp.constants.g / L) * t)
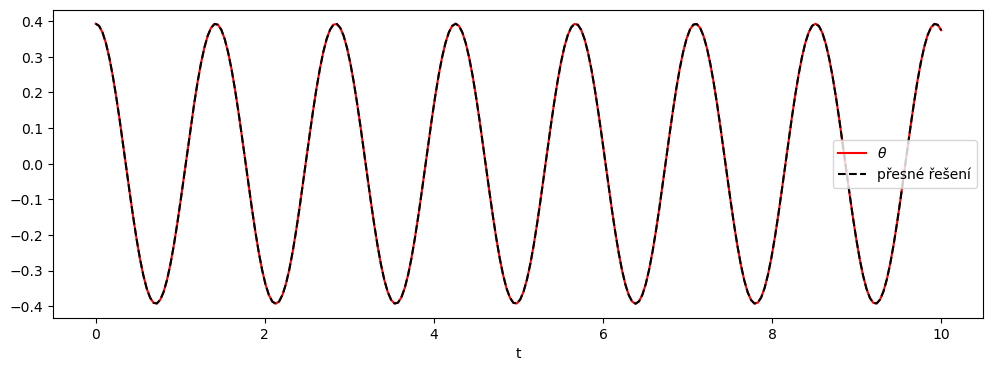
fig, axes = plt.subplots(figsize=(12, 4))
axes.plot(t, x[:, 0], 'r', label=r"$\theta$")
# axes.plot(t, x[:, 1], 'b', label=r"$d\theta / dt$")
axes.plot(t, x_anal, 'k--', label=u"přesné řešení")
axes.legend(loc="best")
axes.set_xlabel("t")
Text(0.5, 0, 't')
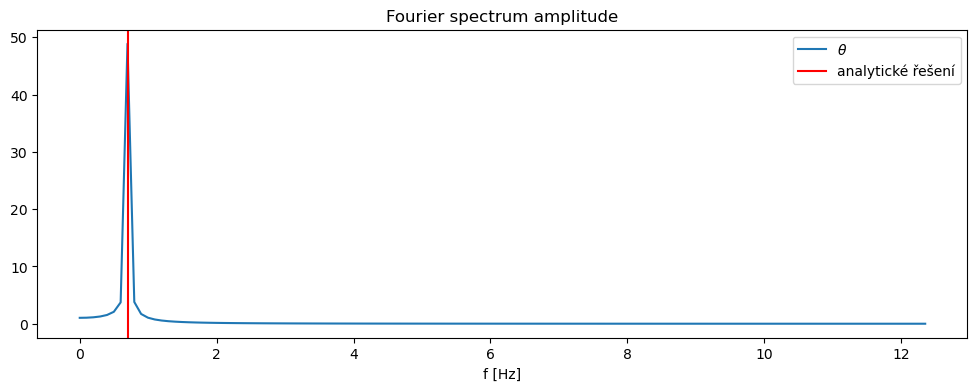
Podívejme se na frekvenční spektrum pomocí FFT.
import scipy.fftpack as fftpack
F = fftpack.fft(x[:,0])
# takto získáme frekvence
w = fftpack.fftfreq(F.shape[0], t[1] - t[0])
w_mask = w >= 0
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(w[w_mask], np.abs(F[w_mask]), label=r"$\theta$")
ax.axvline(np.sqrt(sp.constants.g / L) / (2 * np.pi), color='r', label="analytické řešení")
ax.legend(loc="best")
ax.set_xlabel("f [Hz]")
ax.set_title("Fourier spectrum amplitude")
Text(0.5, 1.0, 'Fourier spectrum amplitude')
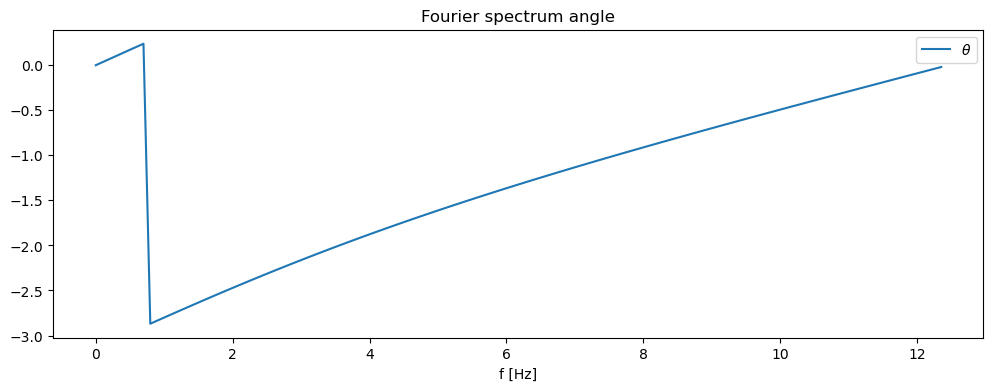
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(w[w_mask], np.angle(F[w_mask]), label=r"$\theta$")
# ax.axvline(sqrt(g/L)/(2*pi), color='r', label=u"analytické řeěení")
ax.legend(loc="best")
ax.set_xlabel("f [Hz]")
ax.set_title("Fourier spectrum angle")
Text(0.5, 1.0, 'Fourier spectrum angle')
Příklad 2: dvojité kyvadlo#
Popis dvojitého kyvadla najdeme např. na Wikipedii: http://en.wikipedia.org/wiki/Double_pendulum
from IPython.display import Image
Image(url='http://upload.wikimedia.org/wikipedia/commons/c/c9/Double-compound-pendulum-dimensioned.svg')
Pohybové rovnice jso:
\({\dot \theta_1} = \frac{6}{m\ell^2} \frac{ 2 p_{\theta_1} - 3 \cos(\theta_1-\theta_2) p_{\theta_2}}{16 - 9 \cos^2(\theta_1-\theta_2)}\)
\({\dot \theta_2} = \frac{6}{m\ell^2} \frac{ 8 p_{\theta_2} - 3 \cos(\theta_1-\theta_2) p_{\theta_1}}{16 - 9 \cos^2(\theta_1-\theta_2)}.\)
\({\dot p_{\theta_1}} = -\frac{1}{2} m \ell^2 \left [ {\dot \theta_1} {\dot \theta_2} \sin (\theta_1-\theta_2) + 3 \frac{g}{\ell} \sin \theta_1 \right ]\)
\({\dot p_{\theta_2}} = -\frac{1}{2} m \ell^2 \left [ -{\dot \theta_1} {\dot \theta_2} \sin (\theta_1-\theta_2) + \frac{g}{\ell} \sin \theta_2 \right]\)
Aby jsme si zjednodušili programování, použijeme notaci \(x = [\theta_1, \theta_2, p_{\theta_1}, p_{\theta_2}]\), takže
\({\dot x_1} = \frac{6}{m\ell^2} \frac{ 2 x_3 - 3 \cos(x_1-x_2) x_4}{16 - 9 \cos^2(x_1-x_2)}\)
\({\dot x_2} = \frac{6}{m\ell^2} \frac{ 8 x_4 - 3 \cos(x_1-x_2) x_3}{16 - 9 \cos^2(x_1-x_2)}\)
\({\dot x_3} = -\frac{1}{2} m \ell^2 \left [ {\dot x_1} {\dot x_2} \sin (x_1-x_2) + 3 \frac{g}{\ell} \sin x_1 \right ]\)
\({\dot x_4} = -\frac{1}{2} m \ell^2 \left [ -{\dot x_1} {\dot x_2} \sin (x_1-x_2) + \frac{g}{\ell} \sin x_2 \right]\)
L = 0.5
m = 0.1
def dx(x, t):
"""
The right-hand side of the pendulum ODE
"""
x1, x2, x3, x4 = x[0], x[1], x[2], x[3]
dx1 = 6.0/(m*L**2) * (2 * x3 - 3 * np.cos(x1-x2) * x4)/(16 - 9 * np.cos(x1-x2)**2)
dx2 = 6.0/(m*L**2) * (8 * x4 - 3 * np.cos(x1-x2) * x3)/(16 - 9 * np.cos(x1-x2)**2)
dx3 = -0.5 * m * L**2 * ( dx1 * dx2 * np.sin(x1-x2) + 3 * (sp.constants.g/L) * np.sin(x1))
dx4 = -0.5 * m * L**2 * (-dx1 * dx2 * np.sin(x1-x2) + (sp.constants.g/L) * np.sin(x2))
return [dx1, dx2, dx3, dx4]
# počáteční stav
x0 = [np.pi/4, np.pi/2, 0, 0]
# časy pro řešení
t = np.linspace(0, 10, 250)
# a konečně řešení
x = sp.integrate.odeint(dx, x0, t)
Nyní použijeme naší znalosti matplotlib a řešení si nakreslíme.
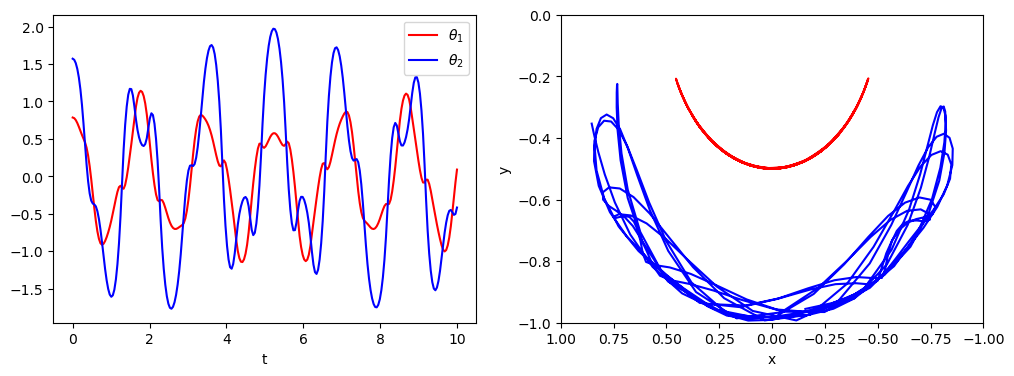
fig, axes = plt.subplots(1,2, figsize=(12,4))
axes[0].plot(t, x[:, 0], 'r', label=r"$\theta_1$")
axes[0].plot(t, x[:, 1], 'b', label=r"$\theta_2$")
axes[0].legend(loc="best")
axes[0].set_xlabel("t")
# teď převedeme úhly na x, y souřadnice
x1 = + L * np.sin(x[:, 0])
y1 = - L * np.cos(x[:, 0])
x2 = x1 + L * np.sin(x[:, 1])
y2 = y1 - L * np.cos(x[:, 1])
# a opět nakreslíme
axes[1].plot(x1, y1, 'r', label="pendulum1")
axes[1].plot(x2, y2, 'b', label="pendulum2")
axes[1].set_ylim([-1, 0])
axes[1].set_xlim([1, -1])
axes[1].set_xlabel("x")
axes[1].set_ylabel("y")
Text(0, 0.5, 'y')
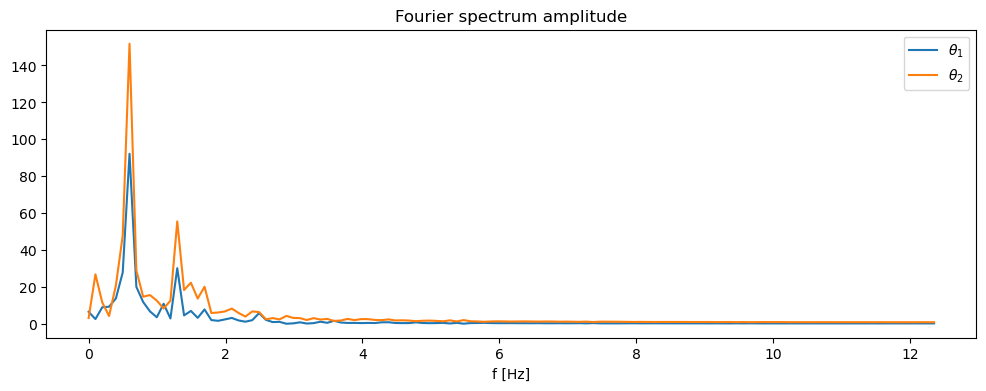
Fourierova transformace pomocí fftpack#
import scipy.fftpack as fftpack
F = fftpack.fft(x[:,0])
F = np.hstack((F[:,np.newaxis], fftpack.fft(x[:,1])[:,np.newaxis]))
# takto získáme frekvence
w = fftpack.fftfreq(F.shape[0], t[1] - t[0])
w_mask = w >= 0
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(w[w_mask], abs(F[w_mask,0]), label=r"$\theta_1$")
ax.plot(w[w_mask], abs(F[w_mask,1]), label=r"$\theta_2$")
ax.legend(loc="best")
ax.set_xlabel("f [Hz]")
ax.set_title("Fourier spectrum amplitude")
Text(0.5, 1.0, 'Fourier spectrum amplitude')
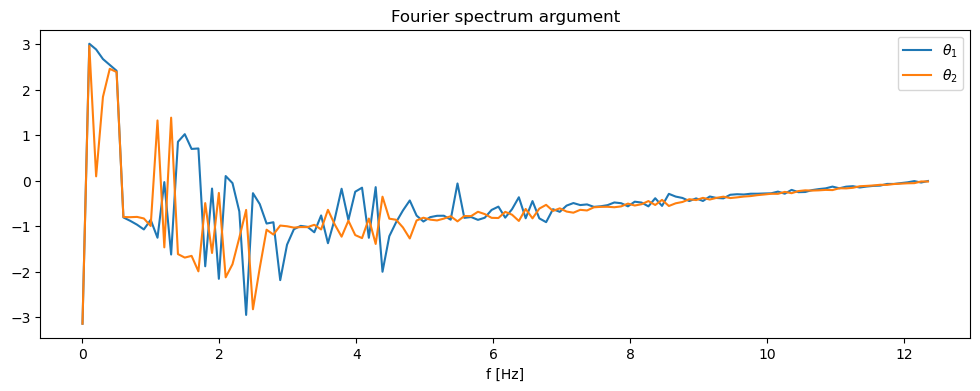
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(w[w_mask], np.angle(F[w_mask,0]), label=r"$\theta_1$")
ax.plot(w[w_mask], np.angle(F[w_mask,1]), label=r"$\theta_2$")
ax.legend(loc="best")
ax.set_xlabel("f [Hz]")
ax.set_title("Fourier spectrum argument")
Text(0.5, 1.0, 'Fourier spectrum argument')
21.5. Lineární algebra#
Modul scipy.linalg obsahuje velké množství nástrojů pro lineární algebru – pro řešení lineárních rovnic, hledání vlastních čísel, různé dekompozice aj. Obsahuje také všechny funkce z numpy.linalg. Více informací viz http://docs.scipy.org/doc/scipy/reference/linalg.html.
import scipy.linalg
Řešení soustavy lineárních rovnic#
n_eq = 3
A = np.random.rand(n_eq, n_eq)
b = np.random.rand(n_eq)
Použijeme funkci solve na řešení soustavy.
x = sp.linalg.solve(A, b)
Stejné řešení pravděpodobně dostaneme pomocí inverzní matice.
xx = np.linalg.inv(A).dot(b)
Co a kdy bude rychlejší?
%%timeit
sp.linalg.solve(A, b)
8.73 μs ± 28.4 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%%timeit
sp.linalg.inv(A).dot(b)
5.04 μs ± 52.3 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Ještě zkontrolujeme řešení.
print("chyba solve = {}".format(np.linalg.norm(A.dot(x) - b)))
print("chyba inv = {}".format(np.linalg.norm(A.dot(xx) - b)))
chyba solve = 7.791361360319881e-16
chyba inv = 3.2053784592957234e-15
Vlastní čísla#
Vlastní čísla matice \(A\) splňují rovnici \(\displaystyle A v_n = \lambda_n v_n\), kde \(v_n\) je \(n\)-tý vlastní vektor a \(\lambda_n\) je \(n\)-té vlastní číslo.
eigvals najde vlastní čísla, eig zároveň i vlstní vektory.
sp.linalg.eigvals(A)
array([ 1.3830469 +0.j, -0.03528554+0.j, 0.54065715+0.j])
evals, evecs = sp.linalg.eig(A)
Vlastní vektory jsou ve sloupcích a v odpovídajícím pořadí k vlastním číslům. Můžeme si to jednoduše ověřit.
for n in range(len(evals)):
print(np.linalg.norm(A.dot(evecs[:,n]) - evals[n] * evecs[:,n]))
4.47545209131181e-16
3.3216670657159767e-16
6.834017936133213e-17
21.6. Řídké matice#
Ŕídké matice osahují jen málé procento nenulových prvků, proto se vyplatí s nimi zacházet speciálním způsobem, včetně uložení v paměti. I s tímto nám SciPy může výrazně pomoci.
import scipy.sparse
import scipy.sparse.linalg
Řídkou matici můžeme vytvořit např. pomocí standardního array obejktu.
# řídká matice uložená běžným způsobem
M = np.array([[1,0,0,0], [0,3,0,0], [0,1,1,0], [1,0,0,1]])
print(M)
[[1 0 0 0]
[0 3 0 0]
[0 1 1 0]
[1 0 0 1]]
# vytvoříme řídkou matici ve formátu CSR (compressed sparse row)
A = sp.sparse.csr_matrix(M)
print(A)
<Compressed Sparse Row sparse matrix of dtype 'int64'
with 6 stored elements and shape (4, 4)>
Coords Values
(0, 0) 1
(1, 1) 3
(2, 1) 1
(2, 2) 1
(3, 0) 1
(3, 3) 1
Efektivnější způsob, jak vyvořit řídkou matici, je vytvožit prázdnou a poté přidávat hodnoty pomocí indexů. Použijeme na to LIL (list of list) formát.
A = sp.sparse.lil_matrix((4,4))
A[0,0] = np.random.rand()
A[1,1] = np.random.rand()
A[1,2] = np.random.rand()
A[2,1] = np.random.rand()
A[2,2] = np.random.rand()
A[3,3] = np.random.rand()
print(A)
<List of Lists sparse matrix of dtype 'float64'
with 6 stored elements and shape (4, 4)>
Coords Values
(0, 0) 0.037233301637553784
(1, 1) 0.5367246128658247
(1, 2) 0.3455197597354325
(2, 1) 0.13455013165727092
(2, 2) 0.27712217699244457
(3, 3) 0.8700405249733052
Takto vytvořenou matici převedeme do CSR formátu, který je obvykle efektivnější, a zkusíme vyřešit lineární systém pomocí konjugovaných gradientů (což nemusí vždy fungovat).
A = sp.sparse.csr_matrix(A)
b = np.random.rand(A.shape[1])
x, info = sp.sparse.linalg.cgs(A, b)
if info == 0:
print("converged solution, error {:.2g}".format(np.linalg.norm(A * x - b)))
print(x)
else:
print("not converged, info = {}".format(info))
converged solution, error 1.3e-14
[23.06803775 1.74106946 0.15624556 0.21287263]
21.7. Interpolace a aproximace#
Scipy nabízí jednoduché možnosti pro interpolaci a aproximaci dat.
import scipy.interpolate
Příklad interpolace#
Vyrobíme si nějaká zašuměná data pomocí známé funkce (např. sin) a zkusíme je interpolovat pomocí interp1d.
def f(x):
return np.sin(x)
n = np.arange(0, 10)
x = np.linspace(0, 9, 100)
y_meas = f(n) + 0.1 * np.random.randn(len(n)) # simulate measurement with noise
y_real = f(x)
linear_interpolation = sp.interpolate.interp1d(n, y_meas)
y_interp1 = linear_interpolation(x)
cubic_interpolation = sp.interpolate.interp1d(n, y_meas, kind='cubic')
y_interp2 = cubic_interpolation(x)
fig, ax = plt.subplots(figsize=(10,4))
ax.plot(n, y_meas, 'bs', label='noisy data')
ax.plot(x, y_real, 'k', lw=2, label='true function')
ax.plot(x, y_interp1, 'r', label='linear interp')
ax.plot(x, y_interp2, 'g', label='cubic interp')
ax.legend(loc=3);
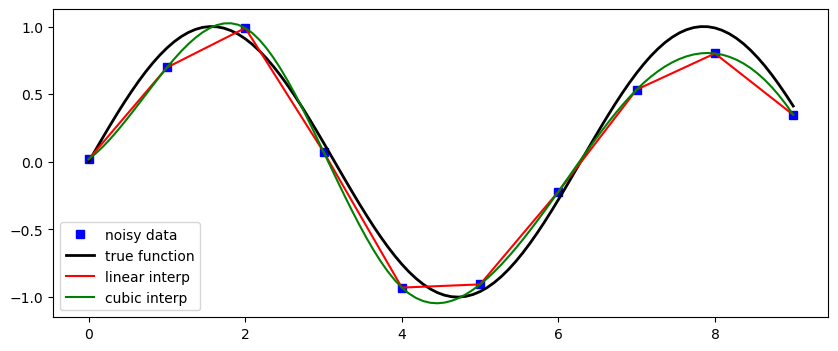
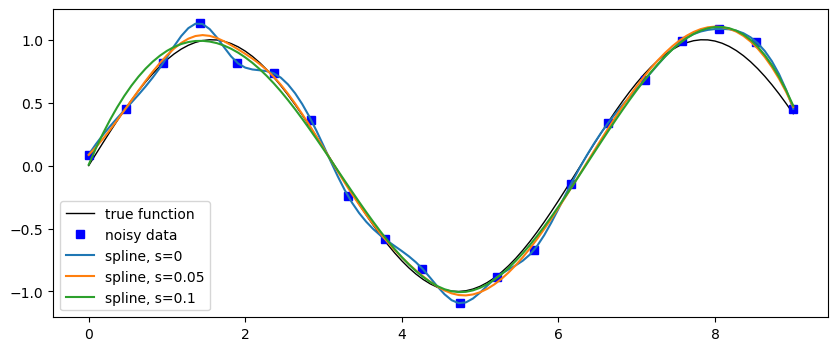
Aproximace pomocí splajnů#
Nyní se podívejme na splajny, které aproximují data, tj. nemusí procházet zadanými body.
x = np.linspace(0, 9, 100)
n = np.linspace(x[0], x[-1], 20)
y_meas = f(n) + 0.1 * np.random.randn(len(n)) # simulate measurement with noise
y_real = f(x)
fig, ax = plt.subplots(figsize=(10,4))
ax.plot(x, y_real, 'k', lw=1, label='true function')
ax.plot(n, y_meas, 'bs', label='noisy data')
for s in (0, 0.05, 0.1):
spline_interpolation = sp.interpolate.UnivariateSpline(n, y_meas, k=3, s=s)
y_spline = spline_interpolation(x)
ax.plot(x, y_spline, label='spline, s={}'.format(s))
ax.legend(loc=3)
<matplotlib.legend.Legend at 0x13a16aae0>
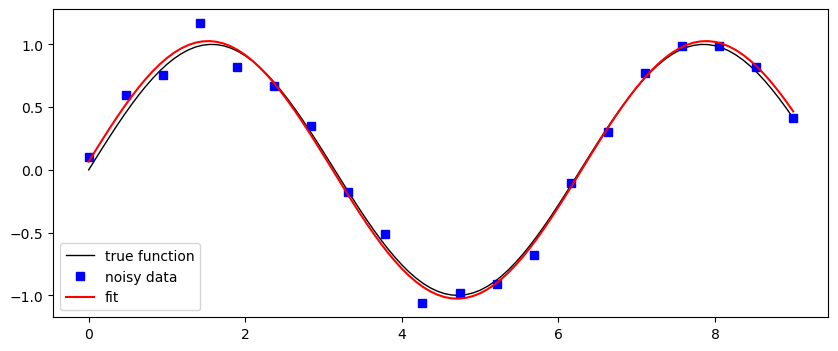
Fit pomocí nejmenších čtverců#
Tohle je trochu jiná úloha než interpolace nebo aproximace. Nyní máme předem danou funkci s neznámými parametry, o které předpokládáme, že popisuje naše data.
# fitování patří do optimalizace
import scipy.optimize
# předpokládáná funkce, a,b,c jsou neznámé parametry
def f_fit(x, a, b, c):
return a*np.sin(b*x + c)
x = np.linspace(0, 9, 100)
n = np.linspace(x[0], x[-1], 20)
y_meas = np.sin(n) + 0.1 * np.random.randn(len(n)) # simulate measurement with noise
y_real = np.sin(x)
# počáteční odhad parametrů
guess = [1.3, 0.7, 1]
params, params_covariance = sp.optimize.curve_fit(f_fit, n, y_meas, guess)
print('výsledek: {:.3g} * sin({:.3g} * x {:+.3g})'.format(*params))
výsledek: 1.03 * sin(0.988 * x +0.0646)
fig, ax = plt.subplots(figsize=(10,4))
ax.plot(x, y_real, 'k', lw=1, label='true function')
ax.plot(n, y_meas, 'bs', label='noisy data')
ax.plot(x, f_fit(x, *params), 'r', label='fit')
ax.legend(loc=3)
<matplotlib.legend.Legend at 0x13fef7b30>
21.8. Zpracovnání obrazu#
from scipy import ndimage, misc
sample = misc.ascent()
samples = [sample]
titles = ["original"]
samples.append(ndimage.shift(sample, (50, 50)))
titles.append("shift")
samples.append(ndimage.shift(sample, (50, 50), mode='nearest'))
titles.append("shift nearest")
samples.append(ndimage.rotate(sample, 30))
titles.append("rotate")
samples.append(sample[50:-50, 50:-50])
titles.append("crop")
/var/folders/dm/gbbql3p121z0tr22r2z98vy00000gn/T/ipykernel_90914/4101079354.py:1: DeprecationWarning: scipy.misc.ascent has been deprecated in SciPy v1.10.0; and will be completely removed in SciPy v1.12.0. Dataset methods have moved into the scipy.datasets module. Use scipy.datasets.ascent instead.
sample = misc.ascent()
fig, axes = plt.subplots(1, len(samples), figsize=(18,6))
for ax, im, tit in zip(axes, samples, titles):
ax.imshow(im, cmap=plt.cm.gray)
ax.set_xticks([])
ax.set_yticks([])
ax.set_title(tit)

from scipy import signal
noisy_sample = sample.copy().astype(np.float64)
noisy_sample += sample.std() * 1 * np.random.standard_normal(sample.shape)
samples = [noisy_sample]
titles = ["noisy"]
samples.append(ndimage.gaussian_filter(noisy_sample, sigma=3))
titles.append("gaussian filter")
samples.append(ndimage.median_filter(noisy_sample, size=5))
titles.append("median filter")
samples.append(signal.wiener(noisy_sample, (5,5)))
titles.append("wiener filter")
fig, axes = plt.subplots(1, len(samples), figsize=(16,5))
for ax, im, tit in zip(axes, samples, titles):
ax.imshow(im, cmap=plt.cm.gray)
ax.set_xticks([])
ax.set_yticks([])
ax.set_title(tit)




