17. Základy NumPy#
NumPy je základní Python knihovna pro práci s numerickými daty, konkrétně s 1- až n-rozměrnými maticemi. Implementace (pro CPython) je z velké části napsána v C a Fortranu a používá BLAS knihovny. Numpy tak umožňuje pracovat s numerickými daty ve stylu Python kontejnerů (existují samozřejmě rozdíly) a zároveň zachovat rychlost kompilovaných jazyků.
V této lekci se dozvíte a naučíte:
Proč potřebujeme
numpypro efektivní práci s numerickými daty.Vytvářet
numpypole.Vektorové a maticové operace s
numpy.array.Užitečné a pokročilejší
numpy“triky”.
Tento notebook byl z části převzat a přeložen z J.R. Johansson: Lectures on scientific computing with Python - díky.
17.1. Importujeme numpy#
Chceme-li použít numpy, je samozřejmě nutné modul importovat. Obvykle se použivá zkratka np:
import numpy as np
17.2. Vytváříme numpy pole (ndarray)#
Existuje několik základních způsobů, jak vytvořit nové numpy pole.
Z nějakého kontejneru typu seznam (
list) nebotuple.Pomocí funkce numpy, která generuje
ndarray, např.zerosneboarange.Načtením ze souboru.
Ze seznamu#
Na seznam použijeme funkci array.
vector = np.array([1, 2, 3, 4])
vector
array([1, 2, 3, 4])
Vícerozměrné pole (matice) se vytvoří z vnořeného seznamu.
matrix = np.array([[1, 2], [3, 4]])
matrix
array([[1, 2],
[3, 4]])
vector a matrix jsou oboje typu ndarray.
type(vector), type(matrix)
(numpy.ndarray, numpy.ndarray)
Rozdíl mezi nimi je jejich rozměr, který dostaneme pomocí shape property (property proto, že shape lze i měnit).
vector.shape
(4,)
matrix.shape
(2, 2)
Počet prvků získáme pomocí size.
matrix.size
4
vector.size
4
Počet dimenzí je v ndim.
matrix.ndim
2
17.3. Proč NumPy?#
Zatím vypadá numpy.ndarray hodně podobně jako (vnořený) seznam. Proč jednoduše tedy jednoduše nepoužívat seznam místo vytváření nového typu?
Existuje několik velmi dobrých důvodů:
Python seznamy jsou příliš obecné. Mohou obsahovat jakýkoliv druh objektu. Jsou dynamicky typované. Nepodporují matematické funkce, jako maticové násobení. Implementating takové funkce pro seznamy by nebylo příliš efektivní.
NumPy pole jsou staticky typovaná a homogenní. Typ prvků je určen při vytvoření pole.
NumPy pole jsou efektivně uložena v paměti.
Díky těmto vlastnostem lze implementovat matematické operace, jako je násobení nebo sčítání, v rychlém, kompilovaném jazyce (C/Fortran). Použití dtype (datový typ) vlastnost ndarray, můžeme vidět, jaký typ dat v poli má:
dtype property vrátí typ prvků v numpy poli.
matrix.dtype
dtype('int64')
Jiný typ do pole uložit nelze:
matrix[0, 0] = "hello"
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[11], line 1
----> 1 matrix[0, 0] = "hello"
ValueError: invalid literal for int() with base 10: 'hello'
Typ prvků můžeme deklarovat explicitně při vytváření pole.
matrix = np.array([[1, 2], [3, 4]], dtype=complex)
matrix
array([[1.+0.j, 2.+0.j],
[3.+0.j, 4.+0.j]])
Běžné (vestavěné) typy pro dtype jsou: int, float, complex, bool, object, atd.
Můžeme také použít jemnější typování numpy typů int64, int16, float16, float128, complex128, aj.
17.4. Pomocné generátory polí#
Zejména velká pole by bylo nepraktické inicializovat pomocí seznamů. Naštěstí v numpy existují funkce, které generují typická pole.
arange vygeneruje posloupnost, syntaxe je stejná jako range
np.arange(0, 10, 1) # argumenty: start, stop, step
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.arange(-1, 0, 0.1)
array([-1. , -0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, -0.2, -0.1])
linspace a logspace vytváří posloupnosti s daným počtem prvků.
# první a poslední prvek jsou obsaženy ve výsledku
np.linspace(0, 10, 5)
array([ 0. , 2.5, 5. , 7.5, 10. ])
np.logspace(0, 10, 11, base=10)
array([1.e+00, 1.e+01, 1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06, 1.e+07,
1.e+08, 1.e+09, 1.e+10])
ones a zeros vytvoří pole ze samých nul nebo jedniček.
np.ones(3)
array([1., 1., 1.])
# pokud chceme 2 a více rozměrů, musíme zadat rozměr jako tuple
np.zeros((2, 3))
array([[0., 0., 0.],
[0., 0., 0.]])
mgrid tvoří pravidelnou mříž.
# všimněte si syntaxe s hranatými závorkami, mgrid se nevolá jako funkce
x, y = np.mgrid[0:2, 0:3]
print(f"x = \n{x}")
print(f"y = \n{y}")
x =
[[0 0 0]
[1 1 1]]
y =
[[0 1 2]
[0 1 2]]
Náhodná data vytvoří funkce random_sample a další z modulu random.
# několik náhodných čísel [0, 1] s rovnoměrným rozdělením
np.random.random_sample(4)
array([0.10626833, 0.00848217, 0.16666784, 0.38809346])
# matice s náhodnými čísly z normálním rozdělením
np.random.standard_normal((4, 4))
array([[ 0.41143888, 0.66513286, -0.49861049, -0.5826634 ],
[ 0.82409279, 1.63102799, -0.7701979 , 1.02740756],
[ 1.58255755, 1.03540015, -0.12739066, 0.59159418],
[ 0.85257566, 0.51737254, -0.22819915, 0.60720876]])
diagflat vytvoří diagonální matici, diagonal vrátí diagonálu matice.
# diagonální matice
diag = np.diagflat([1, 2, 3])
diag
array([[1, 0, 0],
[0, 2, 0],
[0, 0, 3]])
# vrátí diagonálu jako vektor
np.diagonal(diag)
array([1, 2, 3])
Cvičení#
Vytvořte pole 3x4 typu
boolse všemi prvkyTrue.Vytvořte matici 5x5 kde jediné nenulová prvky jsou [1, 2, 3, 4] pod hlavní diagonálou (nápověda - podívejte se na nápovědu funkce
diagflat).
0 0 0 0 0
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
17.5. Práce se soubory#
ASCII soubory#
S textovými (ASCII) soubory obsahující data se setkáváme stále často, přestože to z mnoha důvodů není ideální formát. Na čtení ASCII (spadá sem i CSV) máme v Numpy genfromtxt a loadtxt. V dokumentaci se dozvíte, jak přesně fungují a jaké mají argumenty.
Pomocí %%file vytvoříme soubor ascii_data_1.txt
%%file ascii_data_1.txt
1 -6.1 -6.1 -6.1 1
2 -15.4 -15.4 -15.4 1
3 -15.0 -15.0 -15.0 1
4 -19.3 -19.3 -19.3 1
5 -16.8 -16.8 -16.8 1
6 -11.4 -11.4 -11.4 1
7 -7.6 -7.6 -7.6 1
8 -7.1 -7.1 -7.1 1
9 -10.1 -10.1 -10.1 1
10 -9.5 -9.5 -9.5 1
Overwriting ascii_data_1.txt
Nyní se pokusíme soubor načíst pomocí genfromtxt.
data = np.genfromtxt('ascii_data_1.txt')
print(data)
[[ 1. -6.1 -6.1 -6.1 1. ]
[ 2. -15.4 -15.4 -15.4 1. ]
[ 3. -15. -15. -15. 1. ]
[ 4. -19.3 -19.3 -19.3 1. ]
[ 5. -16.8 -16.8 -16.8 1. ]
[ 6. -11.4 -11.4 -11.4 1. ]
[ 7. -7.6 -7.6 -7.6 1. ]
[ 8. -7.1 -7.1 -7.1 1. ]
[ 9. -10.1 -10.1 -10.1 1. ]
[ 10. -9.5 -9.5 -9.5 1. ]]
loadtxt by mělo fungovat také:
np.loadtxt('ascii_data_1.txt')
array([[ 1. , -6.1, -6.1, -6.1, 1. ],
[ 2. , -15.4, -15.4, -15.4, 1. ],
[ 3. , -15. , -15. , -15. , 1. ],
[ 4. , -19.3, -19.3, -19.3, 1. ],
[ 5. , -16.8, -16.8, -16.8, 1. ],
[ 6. , -11.4, -11.4, -11.4, 1. ],
[ 7. , -7.6, -7.6, -7.6, 1. ],
[ 8. , -7.1, -7.1, -7.1, 1. ],
[ 9. , -10.1, -10.1, -10.1, 1. ],
[ 10. , -9.5, -9.5, -9.5, 1. ]])
savetxt můžeme použít na uložení.
np.savetxt("ascii_data_1_new.txt", data, fmt="%6g")
Soubor můžeme vypsat:
print(open("ascii_data_1_new.txt", "r").read())
1 -6.1 -6.1 -6.1 1
2 -15.4 -15.4 -15.4 1
3 -15 -15 -15 1
4 -19.3 -19.3 -19.3 1
5 -16.8 -16.8 -16.8 1
6 -11.4 -11.4 -11.4 1
7 -7.6 -7.6 -7.6 1
8 -7.1 -7.1 -7.1 1
9 -10.1 -10.1 -10.1 1
10 -9.5 -9.5 -9.5 1
Obecně se snažte textovým souborům (včetně csv apod.) pro numerická datavyhýbat. Jejich formát je vždy do značné míry neurčitý a na disku zabírají zbytečně moc místa. Výhodou je pouze jednoduchost zobrazení v textovém editoru nebo příkazové řadce.
Binární formáty#
Pro numerická data se daleko více hodí binární soubory, které jsou dobře definované a úsporné na místo. Pokud použijeme vhodný a rozšířený formát, nemusíme se bát ani přenositelnosti.
Numpy má vlastní NPY formát. Ten je pochopitelně jednoduchý na používání v NumPy, s přenositelností (pro stále ještě neuživatele Pythonu a obecně další systémy) je to ale už horší. Pomocí save a load můžete jednoduše ukládat a nahrávat Numpy objekty.
np.save("ascii_data_1_new.npy", data)
np.load("ascii_data_1_new.npy")
array([[ 1. , -6.1, -6.1, -6.1, 1. ],
[ 2. , -15.4, -15.4, -15.4, 1. ],
[ 3. , -15. , -15. , -15. , 1. ],
[ 4. , -19.3, -19.3, -19.3, 1. ],
[ 5. , -16.8, -16.8, -16.8, 1. ],
[ 6. , -11.4, -11.4, -11.4, 1. ],
[ 7. , -7.6, -7.6, -7.6, 1. ],
[ 8. , -7.1, -7.1, -7.1, 1. ],
[ 9. , -10.1, -10.1, -10.1, 1. ],
[ 10. , -9.5, -9.5, -9.5, 1. ]])
Velice dobrým a rozšířeným standardem je pak HDF5. Pro Python je jednoduché tento foromát používat pomocí knihovny h5py.
# pokud nemáte h5py nainstalované, můžete jednoduše nainstalovat přímo z notebooku momocí
# %conda install h5py
# nebo pokud používáte pip prostředí
# %pip install h5py
import h5py
V HDF5 souborech jsou data ve stromové struktuře (obdoba aresářů a souborů). Soubor se dvěma datasety můžeme vytvořit např. takto:
with h5py.File("test_hdf5.h5", "w") as hdf5_file:
hdf5_file.create_dataset("data", data=data)
hdf5_file.create_dataset("random", data=np.random.random_sample((3, 4)))
with h5py.File("test_hdf5.h5", "r") as hdf5_file:
# musíme data "nahrát" pomocí [:], jinak by byl výsledek jen "ukazatel" na data
data_hdf5 = hdf5_file["data"][:]
data_hdf5
array([[ 1. , -6.1, -6.1, -6.1, 1. ],
[ 2. , -15.4, -15.4, -15.4, 1. ],
[ 3. , -15. , -15. , -15. , 1. ],
[ 4. , -19.3, -19.3, -19.3, 1. ],
[ 5. , -16.8, -16.8, -16.8, 1. ],
[ 6. , -11.4, -11.4, -11.4, 1. ],
[ 7. , -7.6, -7.6, -7.6, 1. ],
[ 8. , -7.1, -7.1, -7.1, 1. ],
[ 9. , -10.1, -10.1, -10.1, 1. ],
[ 10. , -9.5, -9.5, -9.5, 1. ]])
Jelikož v HDF5 souboru může být velké množství dat (mnoho datasetů, velká data), je čtení dat z HDF5 “lazy”: Dokud data opravdu nepotřebujeme v paměti (např. v NumPy poli), data zůstávají jen v souboru a v paměti máme jen jejich popis, jakýsi ukazatel na data.
To můžete vyzkoušet vymazáním [:] z načítání data v předchozí ukázce.
17.6. Práce s NumPy poli#
Indexování a řezání#
vector = np.linspace(0, 3, 7)
vector
array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ])
Numpy pole můžeme indexovat podobně jako list.
První prvek vektoru:
vector[0]
np.float64(0.0)
matrix = np.array([[1, 2], [3, 4]], dtype=int)
matrix
array([[1, 2],
[3, 4]])
Pro matice můžeme použít rozšířeného indexování - více argumentů pro řez:
matrix[1, 1]
np.int64(4)
Pokud jeden index vynecháme, vrátí numpy N-1 rozměrný řez.
matrix[1]
array([3, 4])
Toho samého docílíme pomocí :
matrix[1, :]
array([3, 4])
První sloupec:
matrix[:, 1]
array([2, 4])
Můžeme také přiřazovat honoty do indexovaných polí.
matrix[0, 0] = -10
print(matrix)
[[-10 2]
[ 3 4]]
Funguje to i pro více prvků:
matrix[1, :] = 0
print(matrix)
[[-10 2]
[ 0 0]]
Řezy mají stejnou syntaxi jako pro seznamy (řezy jsou ostatně koncept Pythonu jako takového). Pro připomenutí, tato syntaxe je [dolní_mez : horní_mez : krok].
my_array = np.arange(1, 10)
my_array
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
Jednoduchý řez s krokem 1:
my_array[1:3]
array([2, 3])
Řez s krokem 2
my_array[:-2:2]
array([1, 3, 5, 7])
Řezy jsou mutable: pokud do nich něco přiřadíme, projeví se to na původním objektu.
my_array[1:3] = [-2, -3]
my_array
array([ 1, -2, -3, 4, 5, 6, 7, 8, 9])
Řezy fungují i pro vícerozměrné matice.
my_array = np.array([[n + m * 10 for n in range(5)] for m in range(5)])
my_array
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])
Část původní matice
my_array[3:, 1:-1]
array([[31, 32, 33],
[41, 42, 43]])
Řez s krokem 2
my_array[::2, ::2]
array([[ 0, 2, 4],
[20, 22, 24],
[40, 42, 44]])
Jetě elegantnější vyřezávání#
Pro řezy můžeme použít nejen čísla, ale také přímo pole. Např. pro výběr některých řádků
row_indices = [1, 2]
my_array[row_indices]
array([[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24]])
Můžeme indexovat i dvěma poli:
my_array[[1, 2, 3], [1, -1, 0]]
array([11, 24, 30])
Můžeme také použít maskování. Např. vytvoříme masku dělitelnosti 3mi.
mask3 = my_array % 3 == 0
print(mask3)
[[ True False False True False]
[False False True False False]
[False True False False True]
[ True False False True False]
[False False True False False]]
Tuto masku pak můžeme použít pro vytvoření řezu.
my_array[mask3]
array([ 0, 3, 12, 21, 24, 30, 33, 42])
Cvičení#
Z pole 8x8 samých nul vyvořte pomocí řezů co nejelegantnějším způsobem 8x8 matici, která vypadá jako šachovnice.
0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1
1 0 1 0 1 0 1 0
Pomocí
np.random.randintvytvořte vektor dvouciferných kladných celých čísel. Poté pomocí indexu typu masky nahraďte liché hodnoty jejich opačnou hodnotou. Např. [11, 20, 42, 33] -> [-11, 20, 42, -33].
17.7. Lineární algebra#
Numpy dokáže velice obratně a efektivně pracovat s vektory, maticemi a n-dimenzionálními poli obecně. Toho je potřeba využívat a kdekoli to je možné použít vektorizovaný kód, tj. co nejvíce formulovat úlohy pomocí vektorových a maticových operací, jako jsou např. násobení matic.
Operace se skaláry#
Jak bychom asi očekávali, skalárem můžeme násobit, dělit, můžeme ho přičítat nebo odečítat.
v1 = np.arange(0, 5)
v1 * 2
array([0, 2, 4, 6, 8])
v1 + 2
array([2, 3, 4, 5, 6])
np.ones((3, 3)) / 4
array([[0.25, 0.25, 0.25],
[0.25, 0.25, 0.25],
[0.25, 0.25, 0.25]])
17.8. Maticové operace po prvcích#
Operace jako násobení, sčítání atd. jsou v numpy stardadně po prvcích, není to tedy klasická maticová (vektorová) algebra.
m1 = np.array([[n + m * 10 for n in range(5)] for m in range(5)])
m1
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])
m1 * m1
array([[ 0, 1, 4, 9, 16],
[ 100, 121, 144, 169, 196],
[ 400, 441, 484, 529, 576],
[ 900, 961, 1024, 1089, 1156],
[1600, 1681, 1764, 1849, 1936]])
v1 * v1
array([ 0, 1, 4, 9, 16])
Pokud se dají pole rozšířit na společný rozměr, numpy to za nás udělá.
v1.shape, m1.shape
((5,), (5, 5))
Výsledek bude mít rozměr m1.shape
m1 * v1
array([[ 0, 1, 4, 9, 16],
[ 0, 11, 24, 39, 56],
[ 0, 21, 44, 69, 96],
[ 0, 31, 64, 99, 136],
[ 0, 41, 84, 129, 176]])
17.9. Maticová algebra#
Klasickou maticovou algebru zajišťuje pro pole typu ndarray operátor @ (PEP-465) nebo funkce dot:
m1 @ m1
array([[ 300, 310, 320, 330, 340],
[1300, 1360, 1420, 1480, 1540],
[2300, 2410, 2520, 2630, 2740],
[3300, 3460, 3620, 3780, 3940],
[4300, 4510, 4720, 4930, 5140]])
# maticové násobení dvou matic
np.dot(m1, m1)
array([[ 300, 310, 320, 330, 340],
[1300, 1360, 1420, 1480, 1540],
[2300, 2410, 2520, 2630, 2740],
[3300, 3460, 3620, 3780, 3940],
[4300, 4510, 4720, 4930, 5140]])
# maticové násobení vektoru a matice
np.dot(m1, v1)
array([ 30, 130, 230, 330, 430])
# skalární součin
v1 @ v1
np.int64(30)
17.10. Transformace#
Už jsme viděli .T pro transponování. Existuje také funkce a metoda transpose. Dále existuje třeba conjugate pro komplexní sdružení.
C = np.array([[1j, 2j], [3j, 4j]])
C
array([[0.+1.j, 0.+2.j],
[0.+3.j, 0.+4.j]])
np.conjugate(C) # nebo C.conjugate()
array([[0.-1.j, 0.-2.j],
[0.-3.j, 0.-4.j]])
# Hermitovské sdružení
C.conjugate().T
array([[0.-1.j, 0.-3.j],
[0.-2.j, 0.-4.j]])
Reálnou a imaginární část dostaneme pomocí real a imag nebo .real a .imag properties:
np.real(C)
array([[0., 0.],
[0., 0.]])
C.imag
array([[1., 2.],
[3., 4.]])
Komplexní číslo rozložíme na absolutní hodnotu a úhel pomocí abs a angle.
np.angle(C+1)
array([[0.78539816, 1.10714872],
[1.24904577, 1.32581766]])
np.abs(C+1)
array([[1.41421356, 2.23606798],
[3.16227766, 4.12310563]])
Cvičení#
Ověřte empiricky na náhodné matici, že platí \((AB)^T = B^T A^T\)
17.11. Základní funkce lineární algebry#
V Numpy existuje modul linalg. Pokročilejší lineární algebru je ale třeba hledat jinde, např. ve SciPy.
Invertovat matici můžeme pomocí linalg.inv.
m2 = np.array([[1., 1.5], [-1, 2]])
m2
array([[ 1. , 1.5],
[-1. , 2. ]])
np.linalg.inv(m2)
array([[ 0.57142857, -0.42857143],
[ 0.28571429, 0.28571429]])
# toto by měla být jednotková matice
np.linalg.inv(m2) @ m2
array([[1., 0.],
[0., 1.]])
linalg.det vypočítá determinant.
np.linalg.det(m2)
np.float64(3.5)
17.12. Zpracování dat#
Numpy je vhodné pro práci se soubory dat, pro které poskytuje řadu funkcí, např. statistických.
Zkusme nějakou statistiku na souboru teplot ve Stockholmu. Data si můžete stáhnout z Gitlabu.
data = np.genfromtxt('data/stockholm_td_adj.dat')
np.shape(data)
(77431, 7)
data[:2, :]
array([[ 1.80e+03, 1.00e+00, 1.00e+00, -6.10e+00, -6.10e+00, -6.10e+00,
1.00e+00],
[ 1.80e+03, 1.00e+00, 2.00e+00, -1.54e+01, -1.54e+01, -1.54e+01,
1.00e+00]])
mean (aritmetický průměr)#
# the temperature data is in column 3
print(
"The daily mean temperature in Stockholm over the last 200 year so has been about {:.1f} °C.".format(
np.mean(data[:, 3])
)
)
The daily mean temperature in Stockholm over the last 200 year so has been about 6.2 °C.
směrodatná odchylka a variance#
np.std(data[:, 3]), np.var(data[:, 3])
(np.float64(8.282271621340573), np.float64(68.59602320966341))
min a max#
# nejnižší denní teplota
data[:, 3].min()
np.float64(-25.8)
# nejvyšší denní teplota
data[:, 3].max()
np.float64(28.3)
sum, prod, trace#
d = np.arange(1, 11)
d
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# sečíst všechny prvky
np.sum(d)
np.int64(55)
# násobek všech prvků
np.prod(d)
np.int64(3628800)
# kumulativní součet
np.cumsum(d)
array([ 1, 3, 6, 10, 15, 21, 28, 36, 45, 55])
# kumulativní násobení
np.cumprod(d)
array([ 1, 2, 6, 24, 120, 720, 5040,
40320, 362880, 3628800])
# stejné jako diag(m1).sum()
np.trace(m1)
np.int64(110)
17.13. Výpočty s částmi polí#
Výpočty můžeme také provádět na podmnožinách dat pomocí indexování (jednoduchého či pokročilého) a dalších metod ukázaných níže.
Vraťme se k údajům o teplotě.
data[1]
array([ 1.80e+03, 1.00e+00, 2.00e+00, -1.54e+01, -1.54e+01, -1.54e+01,
1.00e+00])
Format je: rok, měsíc, den, průměrná teplota, nejnižší teplota, nejvyšší teplota, poloha.
Pokud chceme spočítat průměrnou teplotu v konkrétním měsíci, např únoru, můžeme použít maskování.
np.unique(data[:, 1]) # měsíce mají hodnoty 1 - 12
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12.])
# vytvoříme masku
mask_feb = data[:, 1] == 2
# masku použijeme jako index
print(u"Průměrná únorová teplota je {:.1f} °C".format(np.mean(data[mask_feb, 3])))
Průměrná únorová teplota je -3.2 °C
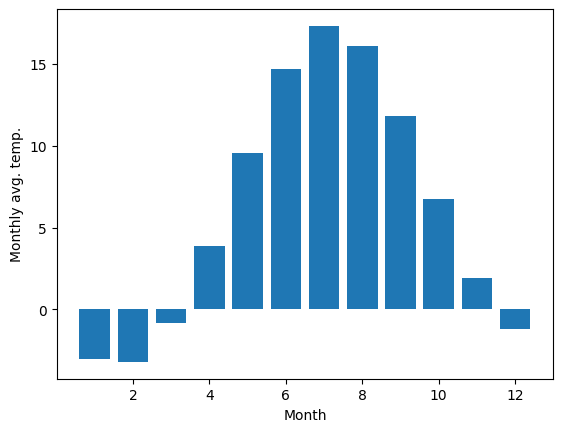
Získání průměrných teplot pro všechny měsíce je také jednoduché.
months = np.arange(1,13)
monthly_mean = [np.mean(data[data[:, 1] == month, 3]) for month in months]
# teď používáme matplotlib, se kterým se naučíme příště :)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.bar(months, monthly_mean)
ax.set_xlabel("Month")
ax.set_ylabel("Monthly avg. temp.");
Výpočty s vícerozměrnými daty#
Pokud je funkce jako min, max apod. použita na vícerozměrné pole, je někdy účelem ji aplikovat na celé pole, jindy zase po řádcích nebo sloupcích. K tomuto účelu slouží argument axis.
m = np.random.rand(3, 4)
m
array([[0.35046271, 0.94457836, 0.3891618 , 0.12152623],
[0.47397166, 0.64313108, 0.43570317, 0.45445978],
[0.76575168, 0.44592918, 0.04877782, 0.13043905]])
# globální max
m.max()
np.float64(0.9445783648825321)
# max pro každý sloupec
m.max(axis=0)
array([0.76575168, 0.94457836, 0.43570317, 0.45445978])
# max pro každý řádek
m.max(axis=1)
array([0.94457836, 0.64313108, 0.76575168])
Argument axis používá mnoho dalších funkcí z numpy.
17.14. Změny rozměrů a spojování polí#
Rozměr Numpy polí může být měněn bez kopírování samotných dat, což výrazně tyto operace zrychluje.
m1
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])
n, m = m1.shape
Např. takto můžeme vytvořit jednorozměrné pole
m1.reshape((1, n*m))
array([[ 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30,
31, 32, 33, 34, 40, 41, 42, 43, 44]])
Nebo použít -1 pro automatické dopočítání
m1.reshape((1, -1))
array([[ 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30,
31, 32, 33, 34, 40, 41, 42, 43, 44]])
Ovšem pozor: jelikož data jsou společná, změna v novém poli se projeví i v původním! Numpy to nazývá views - pohledy.
m2 = m1.reshape((1, -1))
m2[0, 0:5] = 5 # modify the array
m2
array([[ 5, 5, 5, 5, 5, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30,
31, 32, 33, 34, 40, 41, 42, 43, 44]])
Změny se projeví i v původním m1
m1
array([[ 5, 5, 5, 5, 5],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])
Funkce flatten vytvoří jednorozměrné pole (vektor), data jsou v tomto případě kopírována.
m1.flatten()
array([ 5, 5, 5, 5, 5, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31,
32, 33, 34, 40, 41, 42, 43, 44])
Přidávání dimenzí: newaxis#
Pomocí newaxis můžeme jednoduše pomocí řezů přidávat dimenze. Např. převod 1d vektoru na sloupcovou nebo řádkovou matici.
v = np.array([1, 2, 3])
v.shape
(3,)
# vytvoříme sloupec
vc = v[:, np.newaxis]
vc
array([[1],
[2],
[3]])
vc.shape
(3, 1)
# řádek
v[np.newaxis, :].shape
(1, 3)
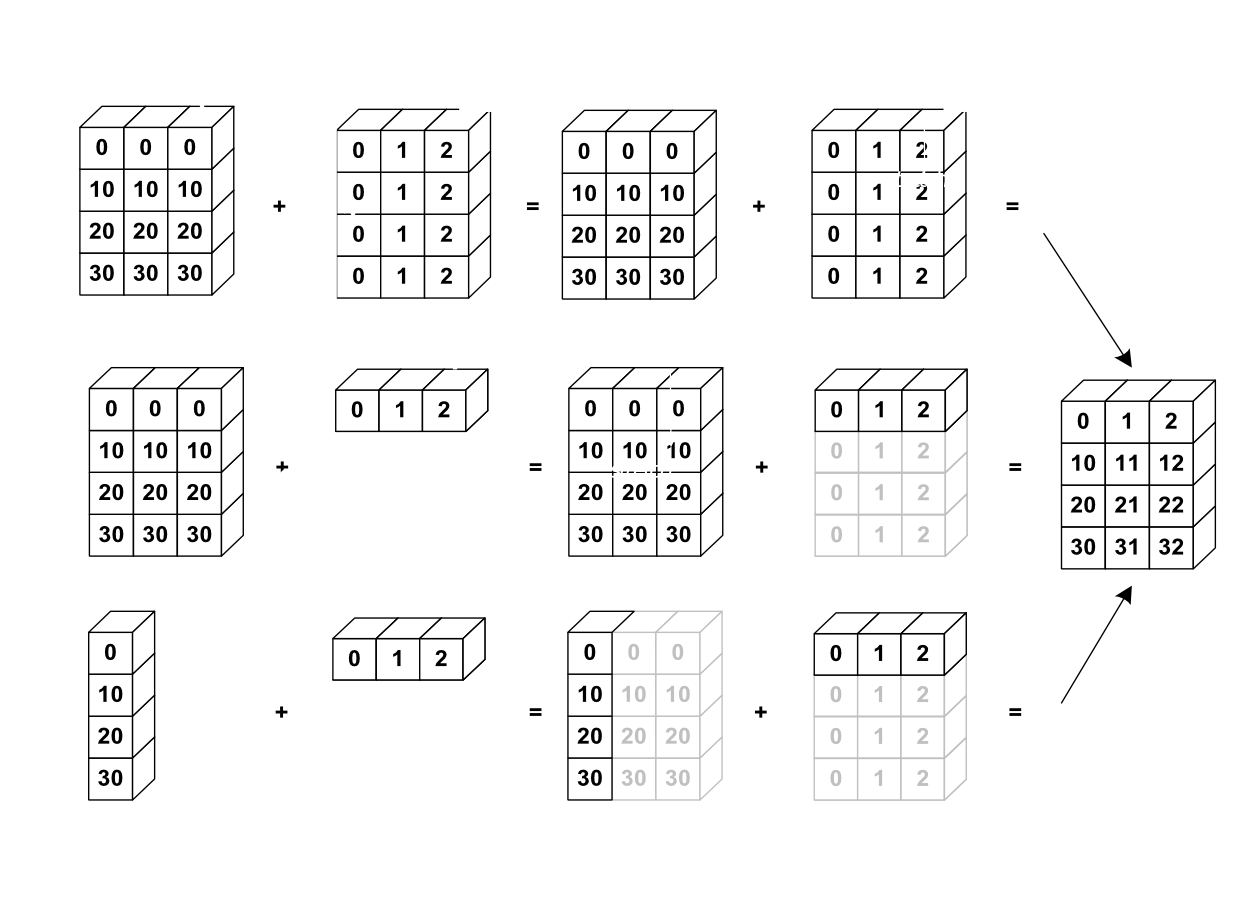
Broadcasting#
Broadcasting je technika, která umožňuje provádět operace mezi poli s různými rozměry, pokud jsou tyto rozměry kompatibilní. Numpy při této operaci optimalizuje rychlost a obvykle i paměť.
Detaily viz dokumentace.
18.  #
#
a = np.array([0, 10, 20, 30])
v = np.array([0, 1, 2])
a[:, np.newaxis] + v
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
18.1. Spojování a opakování#
Na spojování a opakování máme funkce repeat, tile, vstack, hstack a concatenate.
a = np.array([[1, 2], [3, 4]])
a
array([[1, 2],
[3, 4]])
# opakování po prvcích
np.repeat(a, 3)
array([1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4])
# skládání celých polí
np.tile(a, (3, 2))
array([[1, 2, 1, 2],
[3, 4, 3, 4],
[1, 2, 1, 2],
[3, 4, 3, 4],
[1, 2, 1, 2],
[3, 4, 3, 4]])
concatenate spojí dvě pole
b = np.array([[5, 6]])
np.concatenate((a, b), axis=0)
array([[1, 2],
[3, 4],
[5, 6]])
# musíme použít b.T
np.concatenate((a, b.T), axis=1)
array([[1, 2, 5],
[3, 4, 6]])
hstack a vstack skládá pole horizontáleně nebo vertikálně
np.vstack((a, b))
array([[1, 2],
[3, 4],
[5, 6]])
np.hstack((a, b.T))
array([[1, 2, 5],
[3, 4, 6]])
18.2. Cvičení#
Pro náhodné 1D vektory \(u, v\) vypočítejte dyadický součin \(uv\) (\(uv_{ij} = u_iv_j\)) pomocí
newaxis.Vytvořte šachovnicovou matici pomocí
tile.
18.3. Kopírování dat#
Python obecně přiřazuje proměnné pomocí referencí. Numpy objekty nejsou výjimkou.
A = np.array([[1, 2], [3, 4]])
A
array([[1, 2],
[3, 4]])
# B je teď identický objekt s A
B = A
# změna v B se projeví v A
B[0, 0] = 10
A
array([[10, 2],
[ 3, 4]])
Pokud chceme data zkopírovat, tj. pokud bychom chtěli aby A bylo nezávislé na B, můžeme použít metodu nebo funci copy.
B = A.copy()
# nebo B = np.copy(A)
# změny v B už se neprojeví v A
B[0, 0] = -5
A
array([[10, 2],
[ 3, 4]])
18.4. Iterace#
Obecně se iteraci vyhýbáme a přednost dáváme vektorovým operacím (viz níže). Někdy je ale iterace nevyhnutelná.
v = np.array([1, 2, 3, 4])
for element in v:
print(element)
1
2
3
4
Iteruje se přes první index (po řádcích).
M = np.array([[1, 2], [3, 4]])
for row in M:
print("row: {}".format(row))
row: [1 2]
row: [3 4]
Pokud potřebujeme také indexy, použijeme enumerate. (Vzpomínáte?)
for row_idx, row in enumerate(M):
print("row_idx", row_idx, "row", row)
for col_idx, element in enumerate(row):
print("col_idx", col_idx, "element", element)
# update the matrix M: square each element
M[row_idx, col_idx] = element ** 2
row_idx 0 row [1 2]
col_idx 0 element 1
col_idx 1 element 2
row_idx 1 row [3 4]
col_idx 0 element 3
col_idx 1 element 4
# each element in M is now squared
M
array([[ 1, 4],
[ 9, 16]])
18.5. Vektorové funkce#
Jak jsme již říkali, vektorové (vektorizované) funkce jsou obecně daleko rychlejší než iterace. Numpy nám naštěstí cestu od skalární po vektorovou funkci usnadňuje.
def theta(x):
"""
Scalar implemenation of the Heaviside step function.
"""
if x >= 0:
return 1
else:
return 0
# toto bychom chtěli, ale asi to nebude fungovat
theta(np.array([-3, -2, -1, 0, 1, 2, 3]))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[137], line 2
1 # toto bychom chtěli, ale asi to nebude fungovat
----> 2 theta(np.array([-3, -2, -1, 0, 1, 2, 3]))
Cell In[136], line 5, in theta(x)
1 def theta(x):
2 """
3 Scalar implemenation of the Heaviside step function.
4 """
----> 5 if x >= 0:
6 return 1
7 else:
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
Pro vektorizaci naší funkce nám Numpy nabízí vectorize. Tato funkce ale není optimalizovaná pro výkon a primárně slouží pro pohodlné vektorizavání, kdy nám na výkonu nezáleží.
theta_vec = np.vectorize(theta)
theta_vec(np.array([-3, -2, -1, 0, 1, 2, 3]))
array([0, 0, 0, 1, 1, 1, 1])
To bylo celkem snadné … Můžeme také (a pokud to jde tak bychom měli) přepsat naší funkci tak, aby fungovala jak pro skaláry tak pro pole.
def theta_numpy(x):
"""
Vector-aware implemenation of the Heaviside step function.
"""
return 1 * (x >= 0)
theta_numpy(np.array([-3, -2, -1, 0, 1, 2, 3]))
array([0, 0, 0, 1, 1, 1, 1])
# funguje i pro skalár
theta_numpy(-1.2), theta_numpy(2.6)
(0, 1)
Pojďme zkusit porovna rychlost vektorizovaných funkcí. Tipnete si jaká bude rychléjší, případně jak moc rychlejší?
randvec = np.random.random_sample((10000)) * 2000 - 1000
%timeit theta_vec(randvec)
794 μs ± 26.1 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
%timeit theta_numpy(randvec)
10.6 μs ± 196 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
18.6. Používání polí v podmínkách#
Pokud chceme testovat po prvcí, v podmínkách pak použijeme metody all nebo any.
M
array([[ 1, 4],
[ 9, 16]])
# výsledkem M > 5 je pole boolovských hodnot
M > 5
array([[False, False],
[ True, True]])
if (M > 5).any():
print("M obsahuje alespoň jeden prvek větší než 5")
else:
print("M neobsahuje žádný prvek větší než 5")
M obsahuje alespoň jeden prvek větší než 5
if (M > 5).all():
print("všechny prvky v M jsou větší než 5")
else:
print("M obsahuje alespoň jeden prvek menší rovno 5")
M obsahuje alespoň jeden prvek menší rovno 5
18.7. Změna typů#
Numpy pole jsou staticky typované. Pro změnu typu můžeme použít metodu astype (případně asarray).
M.dtype
dtype('int64')
M2 = M.astype(float)
M2
array([[ 1., 4.],
[ 9., 16.]])
M2.dtype
dtype('float64')
M3 = M.astype(bool)
M3
array([[ True, True],
[ True, True]])



