22. Symbolický a sympatický SymPy#
Už jsme viděli mnoho nástrojů pro numerické výpočty. Co ale symbolické výpočty? Každý ví, že derivovat umí i cvičená opice, bude to umět i Python? Nečekaná odpověď je ano. Symbolické výpočty naučil Python Ondřej Čertík v balíku SymPy.
Tento notebook byl z (velké) části převzat a přeložen z J.R. Johansson: Lectures on scientific computing with Python - díky.
22.1. Na úvod#
Někteří z vás možná znáte nějaký systém pro počítačovou algebru (Computer Algebra Systems – CAS), např. Maple, Mathematica, Derive, Maxima, Reduce. Pro Python existují dva velké projekty počítačové algebry:
SymPy - modul který může být použit v jakémkoli Python programu a je dobře podporován v Jupyter Notebook.
Sage - toto je už kompletní (a velice obsáhlý) systém, který si klade za cíl být open source konkurentem komerčním produktům.
My se tady podíváme na některé základní možnosti SymPy.
import matplotlib.pyplot as plt
import numpy as np
import sympy
sympy.init_printing()
22.2. Definujeme symboly#
Pro symbolické výpočty potřebujeme pochopitelně symboly, tak jak jsme zvyklí už z matematiky na základní škole. V Pythonu samotném máme sice proměnné, které jsou v podstatě také symboly, ale operace s nimy se řídí zcela jinými pravidly než potřebujeme pro symbolické výpočty. Naštěstí tu je třída sympy.Symbol.
x = sympy.Symbol('x')
x

Co když napíšeme něco trochu složitějšího.
(sympy.pi + x) / 2

# co jsme to vůbec dostali za typ
type(_)
sympy.core.add.Add
Můžeme také přičadit symbolům nějaké vlastnosti (to se pak pochopitelně může projevit v dalších výpočtech).
a = sympy.Symbol('a', real=True)
a.is_complex
True
b = sympy.Symbol('b', positive=True)
b.is_real
True
b > 0

Zlomky#
r1 = sympy.Rational(4,5)
r2 = sympy.Rational(5,4)
r1, r2

r1 + r2
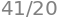
22.3. Vyčíslování#
y = (x + sympy.pi)**2
Numerickou hodnotu můžeme získat pomocí funkce N. Často také využijeme metodu subs:
sympy.N(y.subs(x, 2), 5)
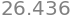
To samé pomocí metody evalf. Pro obojí můžeme zadat počet platných číslic.
sympy.pi.evalf(100)
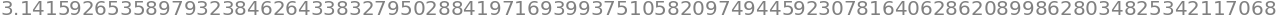
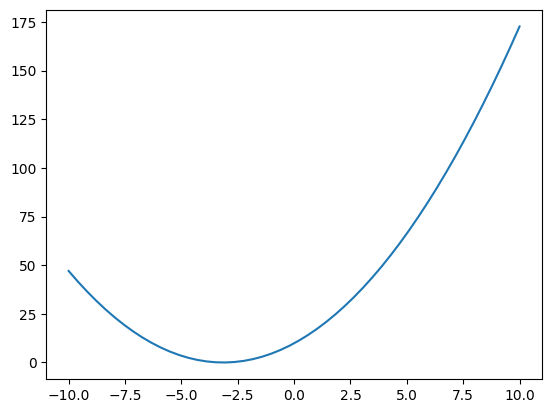
Pokud chceme vytvořit ze symbolického výrazu funkci, použijeme lambdify:
# první argument je seznam proměnných (podobně jako pro lambda funkce)
f_x = sympy.lambdify([x], (x + sympy.pi)**2, 'numpy')
xa = np.linspace(-10, 10)
fix, ax = plt.subplots()
ax.plot(xa, f_x(xa))
[<matplotlib.lines.Line2D at 0x125c4e480>]
22.4. Symbolické úpravy#
Toto je velice důležitá aplikace, která nám může v mnoha případech ušetřit nemálo práce.
Expand a factor#
Začněme pracovat s polynomem, zadaným jako
y = (x+1)*(x+2)*(x+3)
y

Polynom rozvineme pomocí expand:
z = sympy.expand(y)
z

Pomocí factor můžeme dostat zpět původní faktorizovaný výraz.
sympy.factor(z)

expand můžeme použít i pro trigonometrické funkce:
sympy.expand(sympy.sin(a + b), trig=True)

Zjednodušování pomocí simplify#
# tohle by měla být hračka
sympy.simplify(sympy.sin(a)**2 + sympy.cos(a)**2)
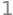
22.5. Derivace a integrály#
SymPy umí symbolicky derivovat (je tedy aspoň tak dobrý jako cvičená opice) a i integrovat.
y = (x**2 + sympy.sin(x))**2
y

sympy.diff(y, x)
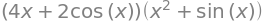
Derivovat můžeme i funkce více proměnných.
x = sympy.Symbol('x')
y = sympy.Symbol('y')
z = sympy.cos(y) * (x**3 + 2*x**2*y)
z
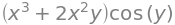
Tohle spočítá
\(\displaystyle \frac{{{{\rm{d}}^3}z}}{{{\rm{d}}x{\rm{d}}{y^2}}} \)
sympy.diff(z, x, 1, y, 2)

Integrace#
f = sympy.sin(x * y) * sympy.cos(x)
f
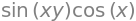
sympy.integrate(f, x)
sympy.integrate(f, y)
22.6. Generace kódu#
Automatická generace kódu vlastnost, kterou oceníme ve chvíli, kdy cheme implementovat naše analytické výsledky v numerické simulaci. Místo abychom začali ručně přepisovat do programovacího jazyka jako je např. Fortran nebo C, může SymPy tuto nezábavnou práci udělat za nás. Navíc při tom neudělá chyby (pravděpodobně).
Pozor, tento module je work in progress.
# řekněme že chceme někde použít tento výsledek
f = sympy.sin( x * y**2) * sympy.exp(y)
f

import sympy.utilities.codegen
f_source = sympy.utilities.codegen.codegen(("f_fortran", f), "F95", "f_fortran")
print(f_source[0][1])
!******************************************************************************
!* Code generated with SymPy 1.13.3 *
!* *
!* See http://www.sympy.org/ for more information. *
!* *
!* This file is part of 'project' *
!******************************************************************************
REAL*8 function f_fortran(x, y)
implicit none
REAL*8, intent(in) :: x
REAL*8, intent(in) :: y
f_fortran = exp(y)*sin(x*y**2)
end function
f_source = sympy.utilities.codegen.codegen(("f_C", f), "C", "f_C")
print(f_source[0][1])
/******************************************************************************
* Code generated with SymPy 1.13.3 *
* *
* See http://www.sympy.org/ for more information. *
* *
* This file is part of 'project' *
******************************************************************************/
#include "f_C.h"
#include <math.h>
double f_C(double x, double y) {
double f_C_result;
f_C_result = exp(y)*sin(x*pow(y, 2));
return f_C_result;
}
22.7. Další možnosti SymPy#
Ukázali jsme si základy práce se symbolickými výpočty pomocí SymPy. Není v našich silách ukázat, co všechno SymPy umí – je toho opravdu hodně. Přehled můžeme získat, podívame-li se na obsah v dokumentaci:
SymPy Core
Combinatorics Module
Number Theory
Concrete Mathematics
Numerical evaluation
Functions Module
Geometry Module
Geometric Algebra Module
Geometric Algebra Module for SymPy
Extended LaTeXModule for SymPy
Symbolic Integrals
Numeric Integrals
Logic Module
Matrices
Mpmath
Polynomials Manipulation Module
Printing System
Plotting Module
Pyglet Plotting Module
Assumptions module
Term rewriting
Series Expansions
Sets
Simplify
Details on the Hypergeometric Function Expansion Module
Statistics
Stats
ODE
PDE
Solvers
Tensor Module
Utilities
Parsing input
Physics Module
Category Theory Module
Differential Geometry Module
Contributions to docs



