Iterators and generators

Comments

Source

Also available in:

Čeština

Iterators are used very often in Python, even though in many cases we do even notice. Generators have become one of the cornerstones of Python 3.

Basic use of iterators and generators

First, we look at how to use iterators in Python. Later, we will learn how they work internally. Simply put, iterators are used to step through the items in an object. What items mean depends on the object. Generator is a type of iterator that dynamically creates (generates) items depending on the internal state (often depending on the last iteration). Hence items are not (necessarily) stored in memory all at once.

Many objects in Python are iterable (can be used to vreate iterators), especially

  • containers: list , tuple, dict, etc.
  • string: str, unicode
  • stream objects, eg. files

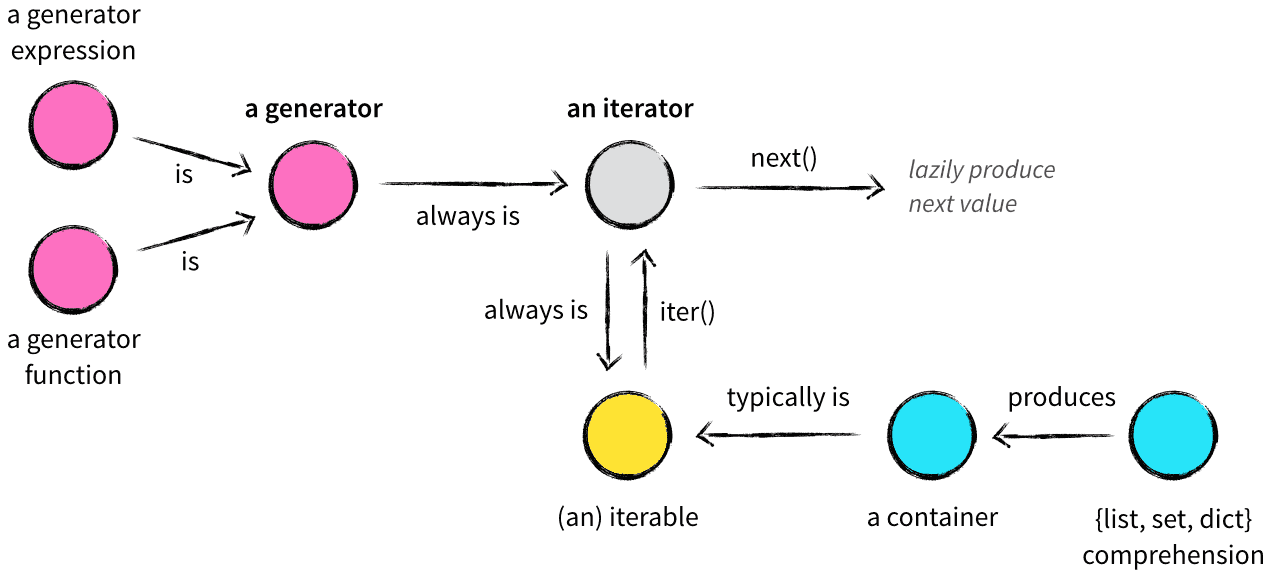
The concept is quite clearly explained in an article Iterables vs. Iterators vs. Generators, from which is the figure.

In [1]:
from IPython.display import Image
Image(url='http://nvie.com/img/relationships.png', width=700)
Out[1]:

for loops

for works in Python solely on the basis of iterators. There is no "classic" for loop counter. Let's demonstrate the syntax on browsing a list.

In [2]:
# first create a list
l = [10, "a", ("x", 1e-3)]
# now browse the items
for x in l:
    print(x)

10
a
('x', 0.001)

We can also browse (iterate) a dictionary - in this case, we get key successively. (But beware: the order of the dictionary elements is random.)

In [3]:
d = {"one": 1, "two": 2}
for k in d:
    print('%s -> %s' % (k, d[k]))

two -> 2
one -> 1

To browse a dictionary, the items method is often useful . Note the use of two variables (in fact it is a tuple but we could omit the paretheses here) in the assignment that is used to decompose, as e.g. in function calls.

In [4]:
d = {"one": 1, "two": 2}
for k, v in d.items():
    print('%s -> %s' % (k, v))

two -> 2
one -> 1

To create a classic for counter, we need to create an object that will gradually return the required numbers. range serves exactly this purpose. (In Python 2, we can also use xrange that returns a generator. In Python 3, range returns generator and xrange does not exist.)

Counters should be the last choice for browsing indexed objects. Use it only if you really need numbers themselves and not the elements.

In [6]:
help(range)
print('range(5) = %s' % range(5))
for x in range(5):
    print(x)

Help on class range in module builtins:

class range(object)
 |  range(stop) -> range object
 |  range(start, stop[, step]) -> range object
 |  
 |  Return a sequence of numbers from start to stop by step.
 |  
 |  Methods defined here:
 |  
 |  __contains__(self, key, /)
 |      Return key in self.
 |  
 |  __eq__(self, value, /)
 |      Return self==value.
 |  
 |  __ge__(self, value, /)
 |      Return self>=value.
 |  
 |  __getattribute__(self, name, /)
 |      Return getattr(self, name).
 |  
 |  __getitem__(self, key, /)
 |      Return self[key].
 |  
 |  __gt__(self, value, /)
 |      Return self>value.
 |  
 |  __hash__(self, /)
 |      Return hash(self).
 |  
 |  __iter__(self, /)
 |      Implement iter(self).
 |  
 |  __le__(self, value, /)
 |      Return self<=value.
 |  
 |  __len__(self, /)
 |      Return len(self).
 |  
 |  __lt__(self, value, /)
 |      Return self<value.
 |  
 |  __ne__(self, value, /)
 |      Return self!=value.
 |  
 |  __new__(*args, **kwargs) from builtins.type
 |      Create and return a new object.  See help(type) for accurate signature.
 |  
 |  __reduce__(...)
 |  
 |  __repr__(self, /)
 |      Return repr(self).
 |  
 |  __reversed__(...)
 |      Return a reverse iterator.
 |  
 |  count(...)
 |      rangeobject.count(value) -> integer -- return number of occurrences of value
 |  
 |  index(...)
 |      rangeobject.index(value, [start, [stop]]) -> integer -- return index of value.
 |      Raise ValueError if the value is not present.
 |  
 |  ----------------------------------------------------------------------
 |  Data descriptors defined here:
 |  
 |  start
 |  
 |  step
 |  
 |  stop

range(5) = range(0, 5)
0
1
2
3
4

If numbering is really needed, we typically need values along with the given index. In this case, use enumerate:

In [7]:
for i, x in enumerate(('egg', 'bacon', 'sausage', 'spam')):
    print('{}. {}'.format(i, x))

0. egg
1. bacon
2. sausage
3. spam

Generator notation

The generator notation can (almost) perform miracles. It is used for an elegant creation of a new object of type list, dict, set or a generator using brackets and keywords for and in, possibly if.

Generator expression

Parenthesis: (expression for variable in iterable)

In [8]:
(x ** 2 for x in range(1, 11))  # creates a generator, i.e. an iterable object
Out[8]:
<generator object <genexpr> at 0x7f6b4816e3a8>

List comprehension

Square brackets: [expression for variable in iterable]

In [9]:
[x ** 2 for x in range(1, 11)]  # creates a list
Out[9]:
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

The same syntax can be used to create a list from a generator.

In [10]:
# create a generator
gen = (x ** 2 for x in range(1, 11))
# and "convert" to a list
[x for x in gen]
Out[10]:
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

Set comprehension

Supported since Python 2.7

Curly brackets: {expression for variable in iterable}

In [11]:
names = ["Ester", "Eva", "Egon", "Marie", "Monika", "Richard"]
first_letters = {name[0] for name in names}
print("The set of initial letters of the names (each only once):\n{}".format(list(first_letters)))

The set of initial letters of the names (each only once):
['M', 'E', 'R']

Dictionary comprehension

Supported since Python 2.7

Curly brackets: {key: value for variable in iterable}

In [12]:
names = ["Ester", "Eva", "Egon", "Marie", "Monika", "Richard"]
# a dictionary of name lengths
{name: len(name) for name in names}
Out[12]:
{'Egon': 4, 'Ester': 5, 'Eva': 3, 'Marie': 5, 'Monika': 6, 'Richard': 7}

Filtering by if

Generator natation can add filtering using the if keyword. As an example, we create two-digit powers of 2.

In [13]:
# create a generator
gen = (2 ** n for n in range(1, 11))
# keep only two-digit numbers
[x for x in gen if 9 < x < 100]
Out[13]:
[16, 32, 64]

Multiple for

A single generator expression can have more for keywords. It will then gradually iterate over all the elements of all iterators. It is the equivalent to nested for loops.

In [14]:
# create doublets from two sets
m1 = {"a", "b", "c"}
m2 = {"a", "c", "e"}
{(x1, x2) for x1 in m1 for x2 in m2}
Out[14]:
{('a', 'a'),
 ('a', 'c'),
 ('a', 'e'),
 ('b', 'a'),
 ('b', 'c'),
 ('b', 'e'),
 ('c', 'a'),
 ('c', 'c'),
 ('c', 'e')}

Exercise

  1. Using a for loop select numbers from 10 to 30 divisible by 3. Print them and store them in a list.
  2. Using the generator notation create two-digit numbers divisible by 3.

Useful functions and methods

zip

zip is used to iterate over several iterables simultaneously. It pairs elements of n objects into n-tuples so that we don't need indexing.

In [15]:
# let's create some generators
l1 = range(1,9)
l2 = (2 ** n for n in l1)
# and interate over them simultaneously
for x, y in zip(l1, l2):
    print("2^%i = %i" % (x, y))

2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256

enumerate

In case you need to know the numeric index of the element, it is better to use enumerate, which gradually returns (index, element) tuples.

In [16]:
for i, n in enumerate(range(1,10)):
    print("index = %i, value = %i" % (i, n))

index = 0, value = 1
index = 1, value = 2
index = 2, value = 3
index = 3, value = 4
index = 4, value = 5
index = 5, value = 6
index = 6, value = 7
index = 7, value = 8
index = 8, value = 9

dict.items

Some classes implement helper methods for iteration. Eg. dict.items returns (key, value) pairs.

In [17]:
# part of the ascii table
d = {i: chr(i) for i in range(40, 50)}
for k, v in d.items():
    print("{0} -> {1}".format(k, v))

48 -> 0
49 -> 1
40 -> (
41 -> )
42 -> *
43 -> +
44 -> ,
45 -> -
46 -> .
47 -> /

itertools module

This module contains many interesting and useful features for creating iterators, often inpired by functional languages.

In [18]:
# list itertools functions
import itertools
sorted([f for f in dir(itertools) if not f.startswith("_")])
Out[18]:
['accumulate',
 'chain',
 'combinations',
 'combinations_with_replacement',
 'compress',
 'count',
 'cycle',
 'dropwhile',
 'filterfalse',
 'groupby',
 'islice',
 'permutations',
 'product',
 'repeat',
 'starmap',
 'takewhile',
 'tee',
 'zip_longest']

The documentation also includes recipes to create more useful features using itertools. Let's look at the example that gets the nth element of an iterator (which of course may not have numeric indexing).

In [19]:
from itertools import islice
# define function
def nth(iterable, n, default=None):
    "Returns the nth item or a default value"
    # note how next is used
    return next(islice(iterable, n, None), default)

# a sample usage
print(nth(range(100), 3))

3

Exercise

  1. For a dict representation of polynomials implement multiplication. $x^3-2x+1$ is represented by {3: 1, 1:-2, 0: 1} .
  2. Implement an equivalent of enumerate using zip (or itertools.izip) and an appropriate function from itertools. Apply to an arbitrarily created list of names and create a dictionary with their ordinal numbers.

The architecture of iterators

The purpose of iterators is to gradually walk through (iterate) an object. The way they are understood and implemented is specific to that object. The key to understanding iterators are two specially named methods __iter__ and __next__ (next in Python 2). They are usually not called directly but eg. using for cycle or generator notation. Let's look at a simple example of the counter.

In [21]:
class Counter(object):
    """A Primitive counter"""
    
    def __init__(self, n):
        # initialize
        # n in the maximum number
        self.n = n
        
    def __iter__(self):
        self.i = 0
        return self
    
    def __next__(self):
        i = self.i
        self.i += 1
        if self.i > self.n:
            raise StopIteration
        return i
   
# use the Counter in a for loop
my_counter = Counter(4)

for a in my_counter:
    print(a)

# create a list using list comprehension
print([a for a in my_counter])

0
1
2
3
[0, 1, 2, 3]

How does it work? By the iterator protocol, which we can show step by step. The first object is created using the method __iter__ (which is called when at the beginning of the for loop or the list comprehension). The built-in function iter calls the __iter__ method.

In [22]:
# iter calls __iter__
it = iter(Counter(5))
print(it)
print(dir(it))

<__main__.Counter object at 0x7f6b48117668>
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__iter__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__next__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'i', 'n']

Then the next (or __next__ in Python 3) method is called. This can be done using the built-in function next:

In [23]:
print(next(it))
print(next(it))

0
1

The iteration ends by a StopIteration exception. It works like this:

In [24]:
it = iter(Counter(4))
while True:
    try:
        print(next(it))
    except StopIteration:
        break

0
1
2
3

Well, now we finally know how "classic" counting for cycles work in Python---using range or xrange iterators. (In Python 2, xrange returns a generator. In Python 3, range a generator and xrange does not exist.)

In [25]:
for i in range(4):
    print(i)

0
1
2
3

In Python, iteration is the fundamental (actually the only) mechanism for loops. If we want to perform an operation on a set of objects, which is typically stored in a container (list, tuple, dict, set etc.) we use iteration.

The architecture of generators

In order to create a generator, or a generator function, there's the yield keyword. Once at the runtime a function encounters yield, the function is "frozen" (maintaining the internal state through a so-called closure) and returns the expression after yield. A generator function call returns an iterator, which controls the start of this function. We show a simple example that just counts forever.

In [28]:
def countup(from_value=0):
    print("This is executed after the first next call")
    while True:
        yield from_value
        from_value += 1
g = countup(2)
In [29]:
next(g)

This is executed after the first next call
Out[29]:
2
In [30]:
next(g)
Out[30]:
3
In [31]:
next(g)
Out[31]:
4

We could go on forever. If we want to stop somewhere, we need to use an exception.

In [32]:
def countupto(to_value, from_value=0):
    while from_value < to_value:
        yield from_value
        from_value += 1
    # this exception can be thrown manually but it is not necessary in this case
    # raise StopIteration
g = countupto(2)
In [33]:
next(g)
Out[33]:
0
In [34]:
next(g)
Out[34]:
1
In [35]:
next(g)

---------------------------------------------------------------------------
StopIteration                             Traceback (most recent call last)
<ipython-input-35-5f315c5de15b> in <module>()
----> 1 next(g)

StopIteration:

The StopIteration exception is caught in for loops, list comprehensions, etc. We can for example do this:

In [36]:
[i for i in countupto(10, 1)]
Out[36]:
[1, 2, 3, 4, 5, 6, 7, 8, 9]

If you try this with countup, the iteration will never end; more precisely, it ends by an error (stack overflow) or overheating the computer.

We have seen the basic creation of generators. The entire protocol is richer and allows you to communicate with generator functions by sending data or by exceptions, see the documentation.

Exercise

  1. Create a generator function that yields numbers that are defined by the recurrent relation $$F_{n}=F_{n-1}+F_{n-2},\ F_0 = 0,\ F_1 = 1$$

Comments

Comments powered by Disqus